Question Number 120964 by bramlexs22 last updated on 04/Nov/20

Commented by bramlexs22 last updated on 04/Nov/20

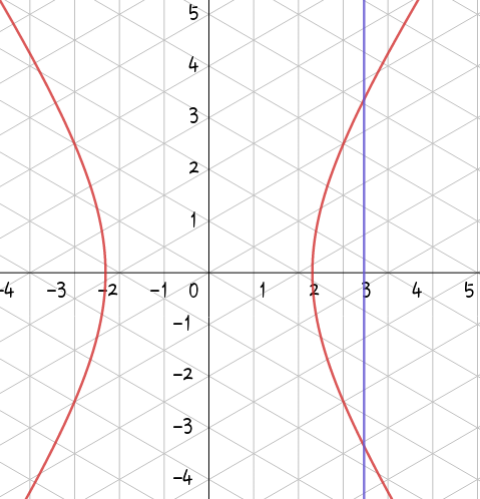
$$\mathrm{the}\:\mathrm{line}\:\mathrm{x}\:=\:\mathrm{3} \\ $$
Commented by liberty last updated on 04/Nov/20
Commented by liberty last updated on 04/Nov/20
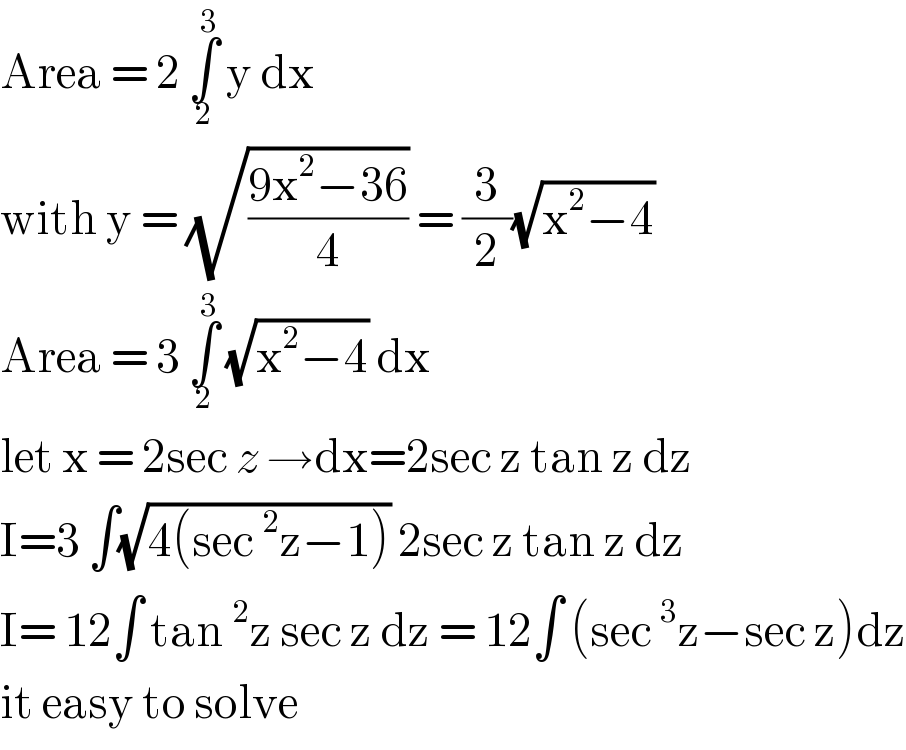
$$\mathrm{Area}\:=\:\mathrm{2}\:\underset{\mathrm{2}} {\overset{\mathrm{3}} {\int}}\:\mathrm{y}\:\mathrm{dx}\: \\ $$$$\mathrm{with}\:\mathrm{y}\:=\:\sqrt{\frac{\mathrm{9x}^{\mathrm{2}} −\mathrm{36}}{\mathrm{4}}}\:=\:\frac{\mathrm{3}}{\mathrm{2}}\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{4}}\: \\ $$$$\mathrm{Area}\:=\:\mathrm{3}\:\underset{\mathrm{2}} {\overset{\mathrm{3}} {\int}}\:\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{4}}\:\mathrm{dx}\: \\ $$$$\mathrm{let}\:\mathrm{x}\:=\:\mathrm{2sec}\:{z}\:\rightarrow\mathrm{dx}=\mathrm{2sec}\:\mathrm{z}\:\mathrm{tan}\:\mathrm{z}\:\mathrm{dz}\: \\ $$$$\mathrm{I}=\mathrm{3}\:\int\sqrt{\mathrm{4}\left(\mathrm{sec}\:^{\mathrm{2}} \mathrm{z}−\mathrm{1}\right)}\:\mathrm{2sec}\:\mathrm{z}\:\mathrm{tan}\:\mathrm{z}\:\mathrm{dz}\:\: \\ $$$$\mathrm{I}=\:\mathrm{12}\int\:\mathrm{tan}\:^{\mathrm{2}} \mathrm{z}\:\mathrm{sec}\:\mathrm{z}\:\mathrm{dz}\:=\:\mathrm{12}\int\:\left(\mathrm{sec}\:^{\mathrm{3}} \mathrm{z}−\mathrm{sec}\:\mathrm{z}\right)\mathrm{dz} \\ $$$$\mathrm{it}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{solve} \\ $$
