Question Number 120970 by Algoritm last updated on 04/Nov/20

Answered by mathmax by abdo last updated on 04/Nov/20
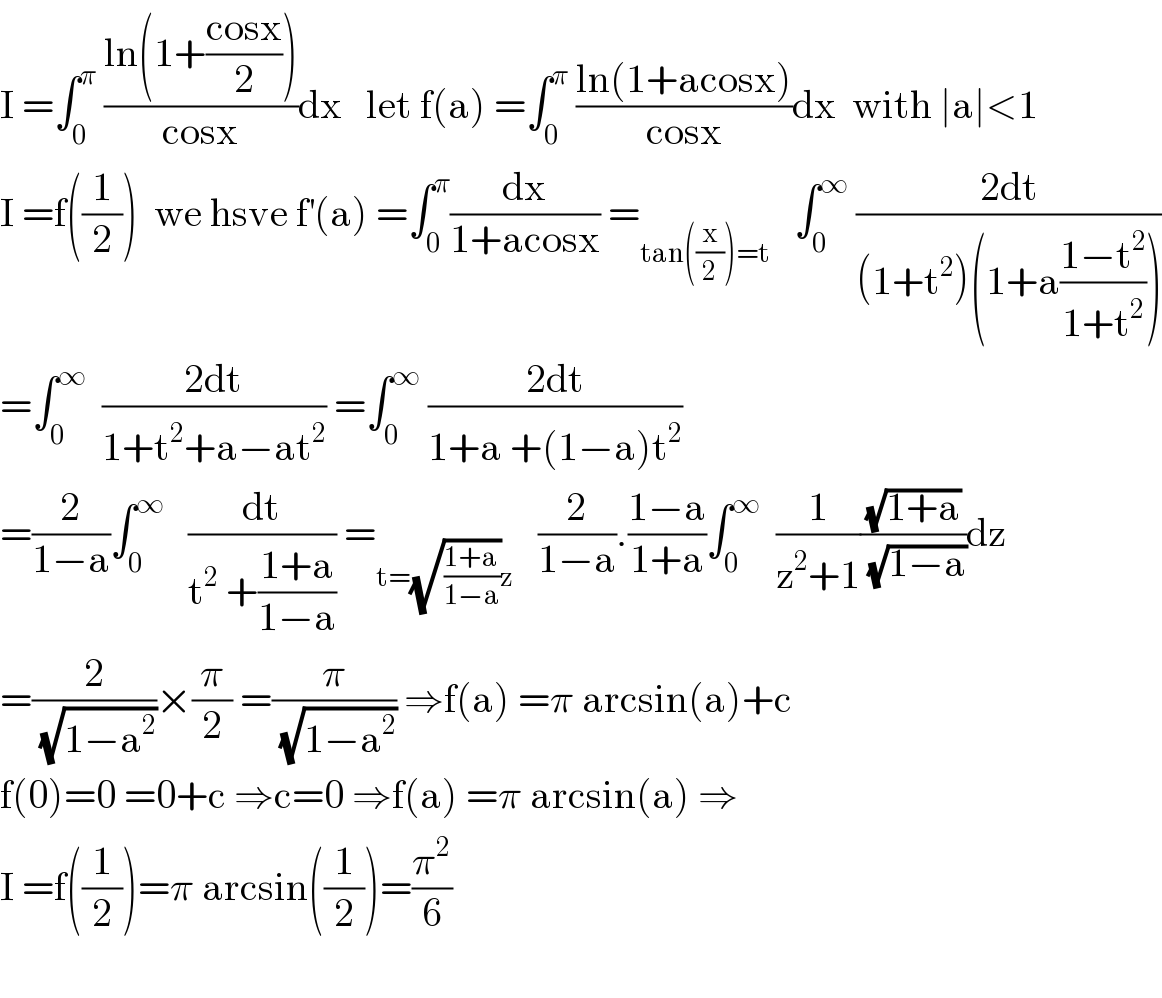
$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{cosx}}{\mathrm{2}}\right)}{\mathrm{cosx}}\mathrm{dx}\:\:\:\mathrm{let}\:\mathrm{f}\left(\mathrm{a}\right)\:=\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{acosx}\right)}{\mathrm{cosx}}\mathrm{dx}\:\:\mathrm{with}\:\mid\mathrm{a}\mid<\mathrm{1} \\ $$$$\mathrm{I}\:=\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:\:\mathrm{we}\:\mathrm{hsve}\:\mathrm{f}^{'} \left(\mathrm{a}\right)\:=\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{dx}}{\mathrm{1}+\mathrm{acosx}}\:=_{\mathrm{tan}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)=\mathrm{t}} \:\:\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{2dt}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{a}\frac{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\right)} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{2dt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} +\mathrm{a}−\mathrm{at}^{\mathrm{2}} }\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{2dt}}{\mathrm{1}+\mathrm{a}\:+\left(\mathrm{1}−\mathrm{a}\right)\mathrm{t}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{2}}{\mathrm{1}−\mathrm{a}}\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} \:+\frac{\mathrm{1}+\mathrm{a}}{\mathrm{1}−\mathrm{a}}}\:=_{\mathrm{t}=\sqrt{\frac{\mathrm{1}+\mathrm{a}}{\mathrm{1}−\mathrm{a}}}\mathrm{z}} \:\:\:\frac{\mathrm{2}}{\mathrm{1}−\mathrm{a}}.\frac{\mathrm{1}−\mathrm{a}}{\mathrm{1}+\mathrm{a}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{2}} +\mathrm{1}}\frac{\sqrt{\mathrm{1}+\mathrm{a}}}{\:\sqrt{\mathrm{1}−\mathrm{a}}}\mathrm{dz} \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}−\mathrm{a}^{\mathrm{2}} }}×\frac{\pi}{\mathrm{2}}\:=\frac{\pi}{\:\sqrt{\mathrm{1}−\mathrm{a}^{\mathrm{2}} }}\:\Rightarrow\mathrm{f}\left(\mathrm{a}\right)\:=\pi\:\mathrm{arcsin}\left(\mathrm{a}\right)+\mathrm{c} \\ $$$$\mathrm{f}\left(\mathrm{0}\right)=\mathrm{0}\:=\mathrm{0}+\mathrm{c}\:\Rightarrow\mathrm{c}=\mathrm{0}\:\Rightarrow\mathrm{f}\left(\mathrm{a}\right)\:=\pi\:\mathrm{arcsin}\left(\mathrm{a}\right)\:\Rightarrow \\ $$$$\mathrm{I}\:=\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\pi\:\mathrm{arcsin}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$$$ \\ $$
