Question Number 121073 by Algoritm last updated on 05/Nov/20
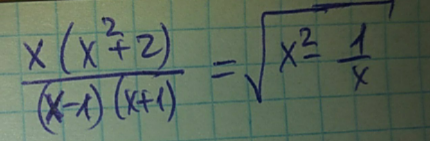
Answered by MJS_new last updated on 05/Nov/20

$$\mathrm{both}\:\mathrm{sides}\:\mathrm{must}\:\mathrm{be}\:\mathrm{greater}\:\mathrm{than}\:\mathrm{or}\:\mathrm{equal}\:\mathrm{to} \\ $$$$\mathrm{zero}\:\Rightarrow\:{x}<\mathrm{0}\wedge{x}\neq−\mathrm{1}\:\vee\:{x}>\mathrm{1} \\ $$$$\mathrm{squaring}\:\mathrm{and}\:\mathrm{transforming}\:\mathrm{leads}\:\mathrm{to} \\ $$$${x}^{\mathrm{5}} +\frac{{x}^{\mathrm{4}} }{\mathrm{6}}+\frac{{x}^{\mathrm{3}} }{\mathrm{2}}−\frac{{x}^{\mathrm{2}} }{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{6}}=\mathrm{0} \\ $$$$\mathrm{trying}\:\mathrm{factors}\:\mathrm{of}\:\frac{\mathrm{1}}{\mathrm{6}}\:\mathrm{we}\:\mathrm{find} \\ $$$${x}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{no}\:\mathrm{other}\:\mathrm{solution};\:\mathrm{the}\:\mathrm{complex}\:\mathrm{solutions}\:\mathrm{of} \\ $$$$\mathrm{the}\:\mathrm{polynome}\:\mathrm{do}\:\mathrm{not}\:\mathrm{solve}\:\mathrm{the}\:\mathrm{given}\:\mathrm{equation} \\ $$
