Question Number 121111 by zakirullah last updated on 05/Nov/20

Commented by benjo_mathlover last updated on 05/Nov/20
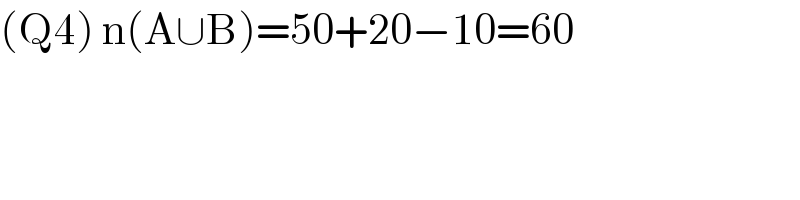
$$\left(\mathrm{Q4}\right)\:\mathrm{n}\left(\mathrm{A}\cup\mathrm{B}\right)=\mathrm{50}+\mathrm{20}−\mathrm{10}=\mathrm{60} \\ $$
Commented by zakirullah last updated on 05/Nov/20

$${great}\:{work} \\ $$
Commented by som(math1967) last updated on 05/Nov/20

$$\mathrm{5}.\:\mathrm{Apple}\:\mathrm{juice}=\mathrm{A} \\ $$$$\:\:\mathrm{Orange}\:\mathrm{juice}=\mathrm{B} \\ $$$$\mathrm{Taking}\:\mathrm{neither}\:\mathrm{Apple}\:\mathrm{juice} \\ $$$$\mathrm{nor}\:\mathrm{Orange}\:\mathrm{juice}=\mathrm{400}−\mathrm{n}\left(\mathrm{A}\cup\mathrm{B}\right) \\ $$$$=\mathrm{400}−\left\{\mathrm{100}+\mathrm{150}−\mathrm{75}\right\} \\ $$$$=\mathrm{400}−\mathrm{175}=\mathrm{225} \\ $$
Commented by zakirullah last updated on 05/Nov/20

$$\boldsymbol{{excellent}}\:\boldsymbol{{sir}}! \\ $$
Commented by som(math1967) last updated on 05/Nov/20
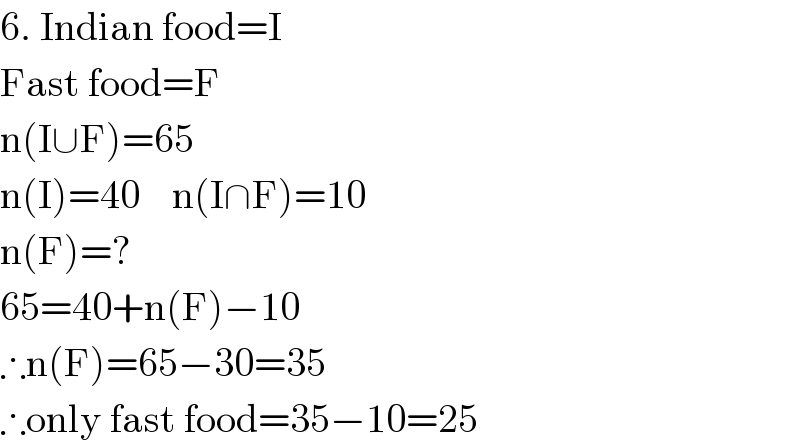
$$\mathrm{6}.\:\mathrm{Indian}\:\mathrm{food}=\mathrm{I} \\ $$$$\mathrm{Fast}\:\mathrm{food}=\mathrm{F} \\ $$$$\mathrm{n}\left(\mathrm{I}\cup\mathrm{F}\right)=\mathrm{65} \\ $$$$\mathrm{n}\left(\mathrm{I}\right)=\mathrm{40}\:\:\:\:\mathrm{n}\left(\mathrm{I}\cap\mathrm{F}\right)=\mathrm{10} \\ $$$$\mathrm{n}\left(\mathrm{F}\right)=? \\ $$$$\mathrm{65}=\mathrm{40}+\mathrm{n}\left(\mathrm{F}\right)−\mathrm{10} \\ $$$$\therefore\mathrm{n}\left(\mathrm{F}\right)=\mathrm{65}−\mathrm{30}=\mathrm{35} \\ $$$$\therefore\mathrm{only}\:\mathrm{fast}\:\mathrm{food}=\mathrm{35}−\mathrm{10}=\mathrm{25} \\ $$
Commented by zakirullah last updated on 05/Nov/20

$${good}\:{work} \\ $$
Commented by zakirullah last updated on 05/Nov/20
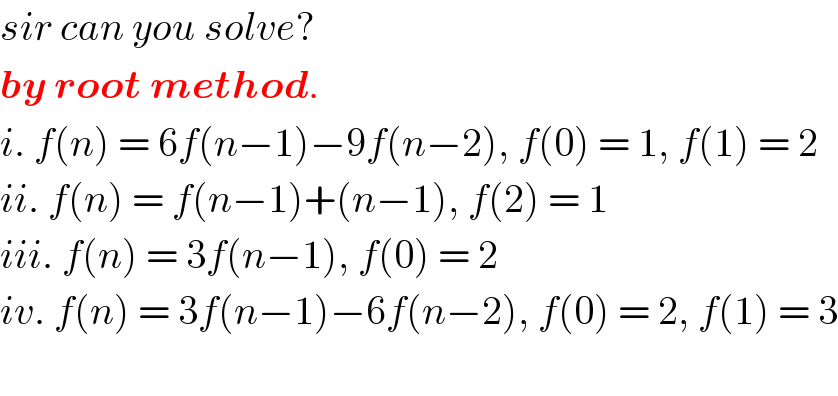
$${sir}\:{can}\:{you}\:{solve}?\: \\ $$$$\boldsymbol{{by}}\:\boldsymbol{{root}}\:\boldsymbol{{method}}. \\ $$$${i}.\:{f}\left({n}\right)\:=\:\mathrm{6}{f}\left({n}−\mathrm{1}\right)−\mathrm{9}{f}\left({n}−\mathrm{2}\right),\:{f}\left(\mathrm{0}\right)\:=\:\mathrm{1},\:{f}\left(\mathrm{1}\right)\:=\:\mathrm{2} \\ $$$${ii}.\:{f}\left({n}\right)\:=\:{f}\left({n}−\mathrm{1}\right)+\left({n}−\mathrm{1}\right),\:{f}\left(\mathrm{2}\right)\:=\:\mathrm{1} \\ $$$${iii}.\:{f}\left({n}\right)\:=\:\mathrm{3}{f}\left({n}−\mathrm{1}\right),\:{f}\left(\mathrm{0}\right)\:=\:\mathrm{2} \\ $$$${iv}.\:{f}\left({n}\right)\:=\:\mathrm{3}{f}\left({n}−\mathrm{1}\right)−\mathrm{6}{f}\left({n}−\mathrm{2}\right),\:{f}\left(\mathrm{0}\right)\:=\:\mathrm{2},\:{f}\left(\mathrm{1}\right)\:=\:\mathrm{3} \\ $$$$ \\ $$
