Menu Close

Question-121328

Tinku Tara 0 Comments
Pin




Question Number 121328 by Maclaurin Stickker last updated on 06/Nov/20
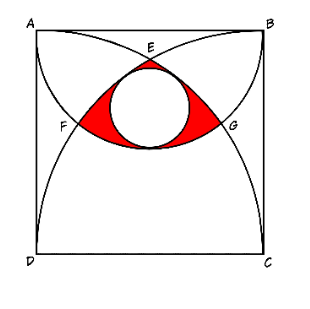
Commented by Maclaurin Stickker last updated on 06/Nov/20
The square has side 1. What is the red area?
$${The}\:{square}\:{has}\:{side}\:\mathrm{1}.\:{What}\:{is}\:{the} \\ $$$${red}\:{area}? \\ $$
Answered by TANMAY PANACEA last updated on 06/Nov/20
(1/4)th circle centre D(0,0) x^2 +y^2 =1^2 s (1/4)th circle centre C(1,0) (x−1)^2 +y^2 =1 semi circle centre((1/(2 )),1) (x−(1/2))^2 +(y−1)^2 =((1/2))^2 ★y=1+(√((1/4)−(x−(1/2))^2 )) ★ point F solve (x−1)^2 +y^2 =1 and (x−(1/2))^2 +(y−1)^2 =(1/4) x^2 −2x+y^2 =0 x^2 −x+(1/4)+y^2 −2y+1=(1/4) −x+2x−2y+1=0 x=2y−1 4y^2 −4y+1−4y+2+y^2 =0 5y^2 −8y+3=0 5y^2 −5y−3y+3=0 5y(y−1)−3(y−1)=0 y=1 and (3/5) so x=1 and (1/5) point F((1/5),(3/5)) G((4/5),(3/5)) point E solve x^2 +y^2 =1 (x−1)^2 +y^2 =1 x^2 =x^2 −2x+1→x=(1/2) E((1/2),((√3)/2)) so area of( red portion+small circle)= ∫_(1/5) ^(1/2) (√(1−(x−1)^2 )) dx+∫_(1/2) ^(4/5) (√(1−x^2 )) dx−∫_(1/5) ^(4/5) 1+(√((1/4)−(x−(1/2))^2 )) dx let the value of this intregal say =p area of small circle is Q so answer will be=P−Q
$$\frac{\mathrm{1}}{\mathrm{4}}{th}\:{circle}\:{centre}\:{D}\left(\mathrm{0},\mathrm{0}\right)\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{1}^{\mathrm{2}} {s} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}{th}\:{circle}\:{centre}\:{C}\left(\mathrm{1},\mathrm{0}\right)\:\left({x}−\mathrm{1}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{1} \\ $$$${semi}\:{circle}\:\:{centre}\left(\frac{\mathrm{1}}{\mathrm{2}\:},\mathrm{1}\right)\:\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left({y}−\mathrm{1}\right)^{\mathrm{2}} =\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\bigstar{y}=\mathrm{1}+\sqrt{\frac{\mathrm{1}}{\mathrm{4}}−\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }\:\bigstar \\ $$$${point}\:{F}\:\:{solve} \\ $$$$\left({x}−\mathrm{1}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{1}\:\:{and}\:\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left({y}−\mathrm{1}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${x}^{\mathrm{2}} −\mathrm{2}{x}+{y}^{\mathrm{2}} =\mathrm{0} \\ $$$${x}^{\mathrm{2}} −{x}+\frac{\mathrm{1}}{\mathrm{4}}+{y}^{\mathrm{2}} −\mathrm{2}{y}+\mathrm{1}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$−{x}+\mathrm{2}{x}−\mathrm{2}{y}+\mathrm{1}=\mathrm{0}\:{x}=\mathrm{2}{y}−\mathrm{1} \\ $$$$\mathrm{4}{y}^{\mathrm{2}} −\mathrm{4}{y}+\mathrm{1}−\mathrm{4}{y}+\mathrm{2}+{y}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{5}{y}^{\mathrm{2}} −\mathrm{8}{y}+\mathrm{3}=\mathrm{0} \\ $$$$\mathrm{5}{y}^{\mathrm{2}} −\mathrm{5}{y}−\mathrm{3}{y}+\mathrm{3}=\mathrm{0} \\ $$$$\mathrm{5}{y}\left({y}−\mathrm{1}\right)−\mathrm{3}\left({y}−\mathrm{1}\right)=\mathrm{0} \\ $$$${y}=\mathrm{1}\:\:{and}\:\frac{\mathrm{3}}{\mathrm{5}}\:\:\:{so}\:{x}=\mathrm{1}\:{and}\:\frac{\mathrm{1}}{\mathrm{5}} \\ $$$${point}\:{F}\left(\frac{\mathrm{1}}{\mathrm{5}},\frac{\mathrm{3}}{\mathrm{5}}\right)\:\:{G}\left(\frac{\mathrm{4}}{\mathrm{5}},\frac{\mathrm{3}}{\mathrm{5}}\right) \\ $$$${point}\:{E} \\ $$$${solve}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{1} \\ $$$$\left({x}−\mathrm{1}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{1} \\ $$$${x}^{\mathrm{2}} ={x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}\rightarrow{x}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${E}\left(\frac{\mathrm{1}}{\mathrm{2}},\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right) \\ $$$${so}\:{area}\:{of}\left(\:{red}\:{portion}+{small}\:{circle}\right)= \\ $$$$\int_{\frac{\mathrm{1}}{\mathrm{5}}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \sqrt{\mathrm{1}−\left({x}−\mathrm{1}\right)^{\mathrm{2}} }\:{dx}+\int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\frac{\mathrm{4}}{\mathrm{5}}} \sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:{dx}−\int_{\frac{\mathrm{1}}{\mathrm{5}}} ^{\frac{\mathrm{4}}{\mathrm{5}}} \mathrm{1}+\sqrt{\frac{\mathrm{1}}{\mathrm{4}}−\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }\:{dx} \\ $$$$\boldsymbol{{let}}\:\boldsymbol{{the}}\:\boldsymbol{{value}}\:\boldsymbol{{of}}\:\boldsymbol{{this}}\:\boldsymbol{{intregal}}\:\boldsymbol{{say}}\:=\boldsymbol{{p}} \\ $$$$\boldsymbol{{area}}\:\boldsymbol{{of}}\:\boldsymbol{{small}}\:\boldsymbol{{circle}}\:\boldsymbol{{is}}\:\boldsymbol{{Q}} \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{answer}}\:\boldsymbol{{will}}\:\boldsymbol{{be}}=\boldsymbol{{P}}−{Q} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *