Question Number 121330 by ajfour last updated on 06/Nov/20
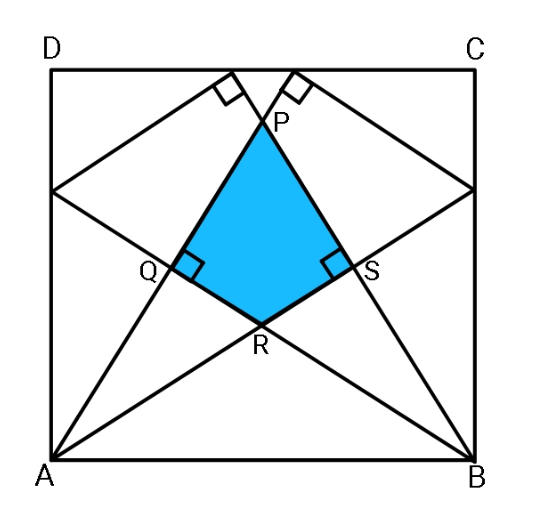
Commented by ajfour last updated on 06/Nov/20

$${Find}\:{ratio}\:{of}\:{coloured}\:{area}\:{to} \\ $$$${outer}\:{square}\:{area}. \\ $$
Commented by MJS_new last updated on 06/Nov/20
$$\mathrm{I}\:\mathrm{think}\:\mathrm{this}\:\mathrm{is}\:\mathrm{not}\:\mathrm{possible}\:\mathrm{in}\:\mathrm{a}\:\mathrm{square}??? \\ $$$$\mathrm{but}\:\mathrm{I}'\mathrm{m}\:\mathrm{tired}\:\mathrm{and}\:\mathrm{maybe}\:\mathrm{I}'\mathrm{m}\:\mathrm{wrong}… \\ $$
Answered by mr W last updated on 07/Nov/20
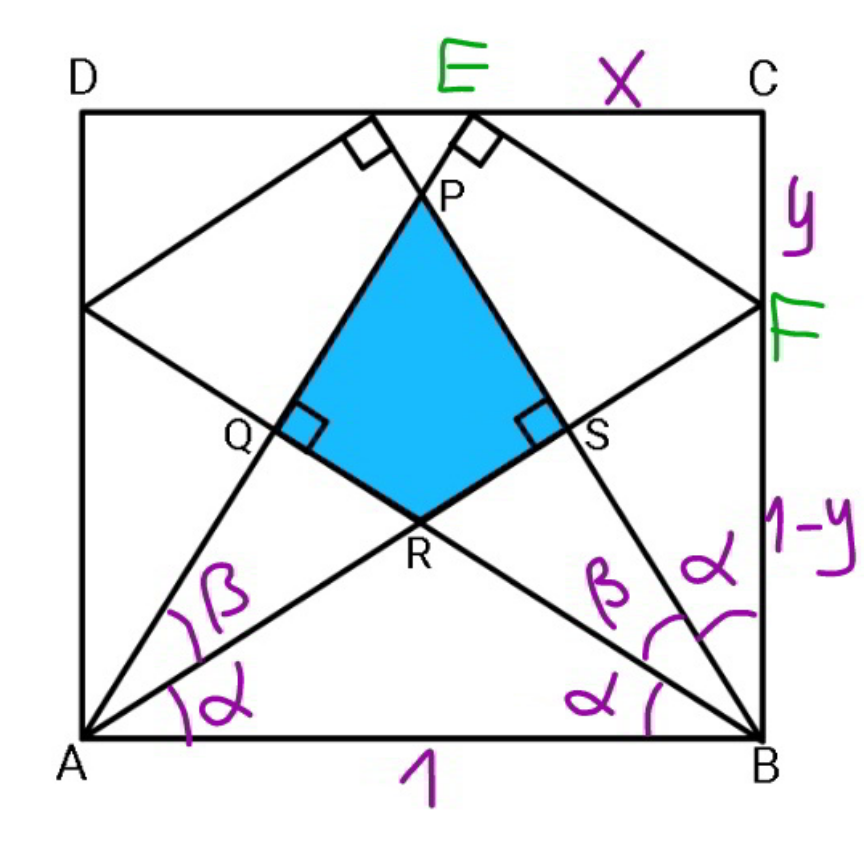
Commented by mr W last updated on 07/Nov/20
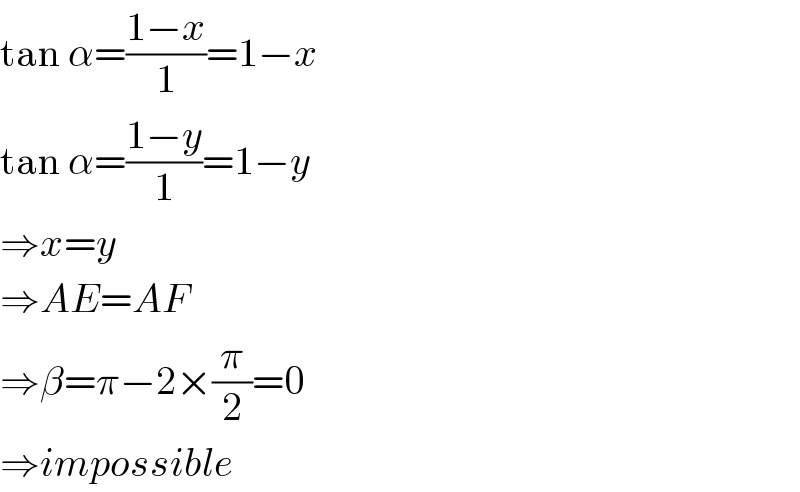
$$\mathrm{tan}\:\alpha=\frac{\mathrm{1}−{x}}{\mathrm{1}}=\mathrm{1}−{x} \\ $$$$\mathrm{tan}\:\alpha=\frac{\mathrm{1}−{y}}{\mathrm{1}}=\mathrm{1}−{y} \\ $$$$\Rightarrow{x}={y} \\ $$$$\Rightarrow{AE}={AF} \\ $$$$\Rightarrow\beta=\pi−\mathrm{2}×\frac{\pi}{\mathrm{2}}=\mathrm{0} \\ $$$$\Rightarrow{impossible} \\ $$
Commented by ajfour last updated on 07/Nov/20
$${thanks}\:{for}\:{attempting}\:{Sir}. \\ $$
