Question-121337

Question Number 121337 by ajfour last updated on 06/Nov/20

Commented by ajfour last updated on 06/Nov/20

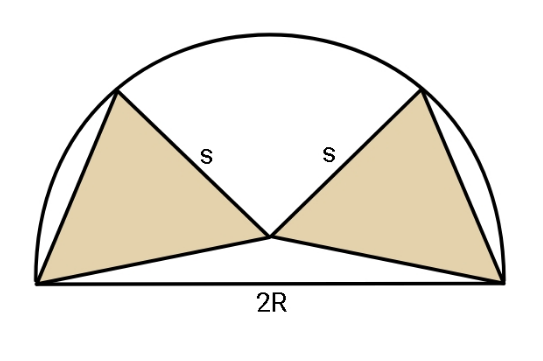
F i n d r a t i o \frac{s}{R}, w h e r e s i s s i d e

l e n g t h s o f t h e t w o e q u i l a t e r a l

t r i a n g l e s a n d R t h e r a d i u s o f

t h e s e m i c i r c l e .

Commented by MJS_new last updated on 06/Nov/20

the common vertex of the triangles is the

center of the circle \Rightarrow s is the radius of this

circle \Rightarrow 2 R ⩽ 2 s \dots please check it!

Commented by ajfour last updated on 07/Nov/20

y e s s i r, v e r y s i l l y q u e s t i o n, p a r d o n m e .

Facebook Tweet Pin