Menu Close

Question-121355

Tinku Tara 0 Comments
Pin




Question Number 121355 by john santu last updated on 07/Nov/20
Answered by liberty last updated on 07/Nov/20
using the formula ⇒(x−x_1 )(x−x_2 )+(y−y_1 )(y−y_2 )=0 where the point (x_1 ,y_1 ) &(x_2 ,y_2 ) are the points of diameter circle ⇔ (x−a)(x−10)+(y−3)(y−6)=0 since the circle passes through the point (2,4) give (2−a)(2−10)+(4−3)(4−6)=0 we get −8(2−a)=2 ; a=2+(1/4)=(9/4) so the equation of circle is (x−(9/4))(x−10)+(y−3)(y−6) = 0 ⇔ x^2 −((49)/4)x+((90)/4) + y^2 −9y+18 = 0 ⇔(x−((49)/8))^2 +(y−(9/2))^2 = ((2401)/(64))+((81)/4)−((90)/4)−18 ⇔(x−((49)/8))^2 +(y−(9/2))^2 = ((2401−144−1152)/(64)) ⇔(x−((49)/8))^2 +(y−(9/2))^2 = ((1105)/(64)) and the equation of diameter passes througt the points A((9/4),3) and B(10,6) is ⇒^(−×(y)) determinant ((((9/4) 3)),((10 6)))_(−×(x)) ⇒3x−((31)/4)y=30−((186)/4) ⇒3x−((31)/4)y +((66)/4)=0 or 12x−31y+66=0
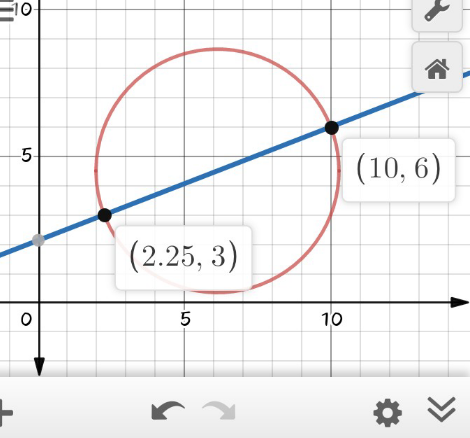
$$\mathrm{using}\:\mathrm{the}\:\mathrm{formula}\:\Rightarrow\left(\mathrm{x}−\mathrm{x}_{\mathrm{1}} \right)\left(\mathrm{x}−\mathrm{x}_{\mathrm{2}} \right)+\left(\mathrm{y}−\mathrm{y}_{\mathrm{1}} \right)\left(\mathrm{y}−\mathrm{y}_{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\mathrm{where}\:\mathrm{the}\:\mathrm{point}\:\left(\mathrm{x}_{\mathrm{1}} ,\mathrm{y}_{\mathrm{1}} \right)\:\&\left(\mathrm{x}_{\mathrm{2}} ,\mathrm{y}_{\mathrm{2}} \right)\:\mathrm{are}\: \\ $$$$\mathrm{the}\:\mathrm{points}\:\mathrm{of}\:\mathrm{diameter}\:\mathrm{circle} \\ $$$$\Leftrightarrow\:\left(\mathrm{x}−\mathrm{a}\right)\left(\mathrm{x}−\mathrm{10}\right)+\left(\mathrm{y}−\mathrm{3}\right)\left(\mathrm{y}−\mathrm{6}\right)=\mathrm{0} \\ $$$$\mathrm{since}\:\mathrm{the}\:\mathrm{circle}\:\mathrm{passes}\:\mathrm{through}\:\mathrm{the}\:\mathrm{point} \\ $$$$\left(\mathrm{2},\mathrm{4}\right)\:\mathrm{give}\:\left(\mathrm{2}−\mathrm{a}\right)\left(\mathrm{2}−\mathrm{10}\right)+\left(\mathrm{4}−\mathrm{3}\right)\left(\mathrm{4}−\mathrm{6}\right)=\mathrm{0} \\ $$$$\mathrm{we}\:\mathrm{get}\:−\mathrm{8}\left(\mathrm{2}−\mathrm{a}\right)=\mathrm{2}\:;\:\mathrm{a}=\mathrm{2}+\frac{\mathrm{1}}{\mathrm{4}}=\frac{\mathrm{9}}{\mathrm{4}} \\ $$$$\mathrm{so}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{circle}\:\mathrm{is}\: \\ $$$$\left(\mathrm{x}−\frac{\mathrm{9}}{\mathrm{4}}\right)\left(\mathrm{x}−\mathrm{10}\right)+\left(\mathrm{y}−\mathrm{3}\right)\left(\mathrm{y}−\mathrm{6}\right)\:=\:\mathrm{0} \\ $$$$\Leftrightarrow\:\mathrm{x}^{\mathrm{2}} −\frac{\mathrm{49}}{\mathrm{4}}\mathrm{x}+\frac{\mathrm{90}}{\mathrm{4}}\:+\:\mathrm{y}^{\mathrm{2}} −\mathrm{9y}+\mathrm{18}\:=\:\mathrm{0} \\ $$$$\Leftrightarrow\left(\mathrm{x}−\frac{\mathrm{49}}{\mathrm{8}}\right)^{\mathrm{2}} +\left(\mathrm{y}−\frac{\mathrm{9}}{\mathrm{2}}\right)^{\mathrm{2}} =\:\frac{\mathrm{2401}}{\mathrm{64}}+\frac{\mathrm{81}}{\mathrm{4}}−\frac{\mathrm{90}}{\mathrm{4}}−\mathrm{18} \\ $$$$\Leftrightarrow\left(\mathrm{x}−\frac{\mathrm{49}}{\mathrm{8}}\right)^{\mathrm{2}} +\left(\mathrm{y}−\frac{\mathrm{9}}{\mathrm{2}}\right)^{\mathrm{2}} =\:\frac{\mathrm{2401}−\mathrm{144}−\mathrm{1152}}{\mathrm{64}} \\ $$$$\Leftrightarrow\left(\mathrm{x}−\frac{\mathrm{49}}{\mathrm{8}}\right)^{\mathrm{2}} +\left(\mathrm{y}−\frac{\mathrm{9}}{\mathrm{2}}\right)^{\mathrm{2}} =\:\frac{\mathrm{1105}}{\mathrm{64}} \\ $$$$\mathrm{and}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{diameter}\:\mathrm{passes}\:\mathrm{througt} \\ $$$$\mathrm{the}\:\mathrm{points}\:\mathrm{A}\left(\frac{\mathrm{9}}{\mathrm{4}},\mathrm{3}\right)\:\mathrm{and}\:\mathrm{B}\left(\mathrm{10},\mathrm{6}\right)\:\mathrm{is}\: \\ $$$$\Rightarrow^{−×\left({y}\right)} \begin{vmatrix}{\frac{\mathrm{9}}{\mathrm{4}}\:\:\:\:\:\mathrm{3}}\\{\mathrm{10}\:\:\:\:\:\mathrm{6}}\end{vmatrix}_{−×\left({x}\right)} \Rightarrow\mathrm{3x}−\frac{\mathrm{31}}{\mathrm{4}}\mathrm{y}=\mathrm{30}−\frac{\mathrm{186}}{\mathrm{4}} \\ $$$$\Rightarrow\mathrm{3x}−\frac{\mathrm{31}}{\mathrm{4}}\mathrm{y}\:+\frac{\mathrm{66}}{\mathrm{4}}=\mathrm{0}\:\mathrm{or}\:\mathrm{12x}−\mathrm{31y}+\mathrm{66}=\mathrm{0} \\ $$
Commented by john santu last updated on 07/Nov/20

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *