Question-121397

Question Number 121397 by abdelsalamalmukasabe last updated on 07/Nov/20

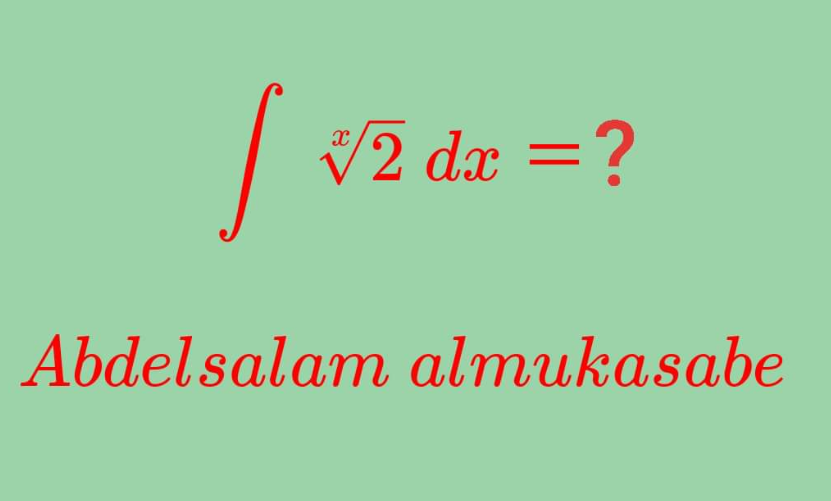
Answered by MJS_new last updated on 07/Nov/20

∫2^(1/x) dx= [by parts] =2^(1/x) x+ln 2 ∫(2^(1/x) /x)dx= [t=(1/x) → dx=−x^2 dt] =2^(1/x) x−ln 2 ∫(2^t /t)dt= =2^(1/x) x−ln 2 Ei (ln 2 t) = =2^(1/x) x−ln 2 Ei (((ln 2)/x)) +C

$$\int\mathrm{2}^{\mathrm{1}/{x}} {dx}= \\ $$$$\:\:\:\:\:\left[\mathrm{by}\:\mathrm{parts}\right] \\ $$$$=\mathrm{2}^{\mathrm{1}/{x}} {x}+\mathrm{ln}\:\mathrm{2}\:\int\frac{\mathrm{2}^{\mathrm{1}/{x}} }{{x}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{\mathrm{1}}{{x}}\:\rightarrow\:{dx}=−{x}^{\mathrm{2}} {dt}\right] \\ $$$$=\mathrm{2}^{\mathrm{1}/{x}} {x}−\mathrm{ln}\:\mathrm{2}\:\int\frac{\mathrm{2}^{{t}} }{{t}}{dt}= \\ $$$$=\mathrm{2}^{\mathrm{1}/{x}} {x}−\mathrm{ln}\:\mathrm{2}\:\mathrm{Ei}\:\left(\mathrm{ln}\:\mathrm{2}\:{t}\right)\:= \\ $$$$=\mathrm{2}^{\mathrm{1}/{x}} {x}−\mathrm{ln}\:\mathrm{2}\:\mathrm{Ei}\:\left(\frac{\mathrm{ln}\:\mathrm{2}}{{x}}\right)\:+{C} \\ $$

Answered by mathmax by abdo last updated on 07/Nov/20

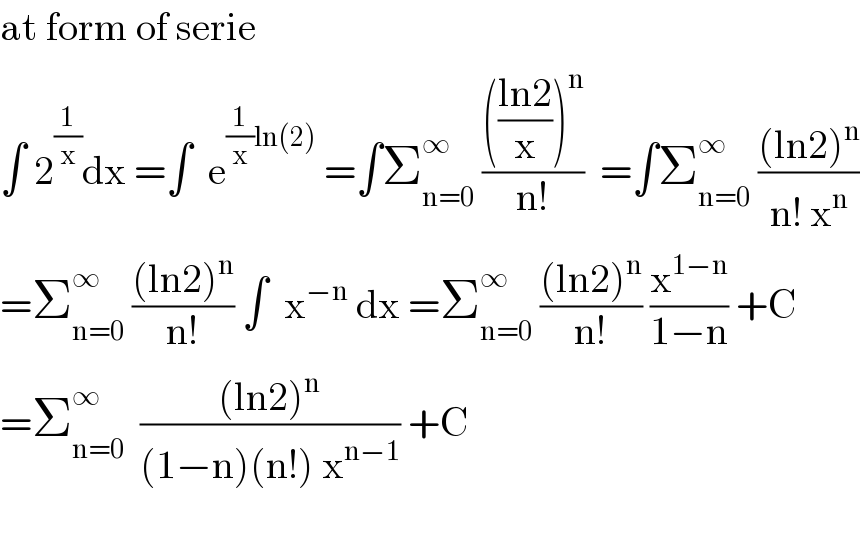
at form of serie ∫ 2^(1/x) dx =∫ e^((1/x)ln(2)) =∫Σ_(n=0) ^∞ (((((ln2)/x))^n )/(n!)) =∫Σ_(n=0) ^∞ (((ln2)^n )/(n! x^n )) =Σ_(n=0) ^∞ (((ln2)^n )/(n!)) ∫ x^(−n) dx =Σ_(n=0) ^∞ (((ln2)^n )/(n!)) (x^(1−n) /(1−n)) +C =Σ_(n=0) ^∞ (((ln2)^n )/((1−n)(n!) x^(n−1) )) +C

$$\mathrm{at}\:\mathrm{form}\:\mathrm{of}\:\mathrm{serie} \\ $$$$\int\:\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{x}}} \mathrm{dx}\:=\int\:\:\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}}\mathrm{ln}\left(\mathrm{2}\right)} \:=\int\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(\frac{\mathrm{ln2}}{\mathrm{x}}\right)^{\mathrm{n}} }{\mathrm{n}!}\:\:=\int\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(\mathrm{ln2}\right)^{\mathrm{n}} }{\mathrm{n}!\:\mathrm{x}^{\mathrm{n}} } \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(\mathrm{ln2}\right)^{\mathrm{n}} }{\mathrm{n}!}\:\int\:\:\mathrm{x}^{−\mathrm{n}} \:\mathrm{dx}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(\mathrm{ln2}\right)^{\mathrm{n}} }{\mathrm{n}!}\:\frac{\mathrm{x}^{\mathrm{1}−\mathrm{n}} }{\mathrm{1}−\mathrm{n}}\:+\mathrm{C} \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left(\mathrm{ln2}\right)^{\mathrm{n}} }{\left(\mathrm{1}−\mathrm{n}\right)\left(\mathrm{n}!\right)\:\mathrm{x}^{\mathrm{n}−\mathrm{1}} }\:+\mathrm{C} \\ $$$$ \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply