Question-121461

Question Number 121461 by bramlexs22 last updated on 08/Nov/20

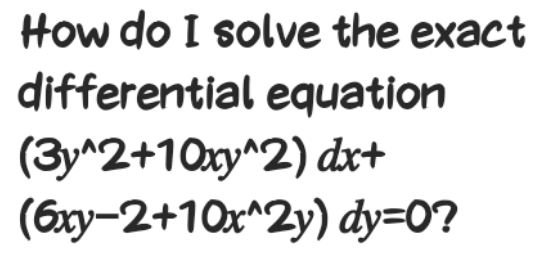
Answered by Olaf last updated on 08/Nov/20

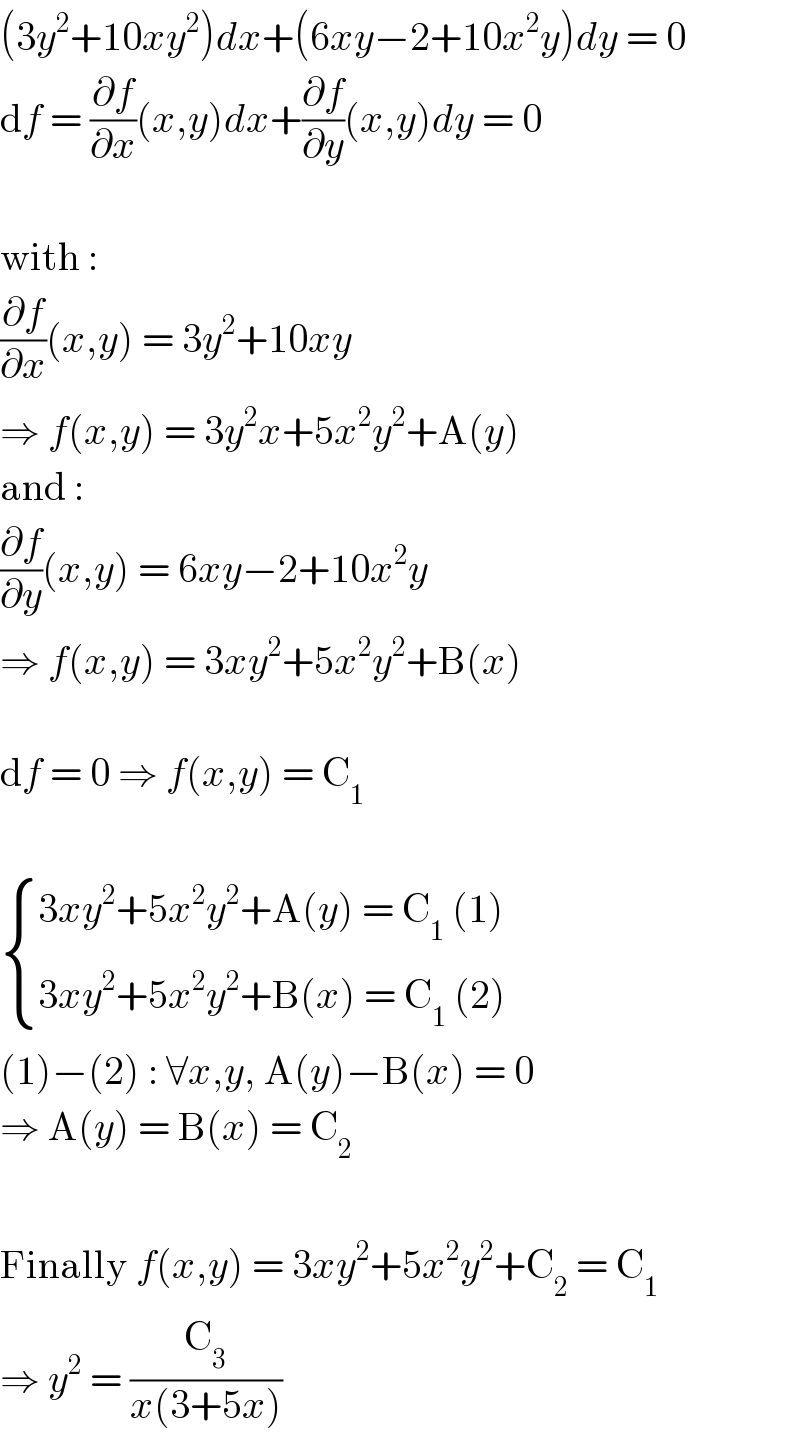
(3y^2 +10xy^2 )dx+(6xy−2+10x^2 y)dy = 0 df = (∂f/∂x)(x,y)dx+(∂f/∂y)(x,y)dy = 0 with : (∂f/∂x)(x,y) = 3y^2 +10xy ⇒ f(x,y) = 3y^2 x+5x^2 y^2 +A(y) and : (∂f/∂y)(x,y) = 6xy−2+10x^2 y ⇒ f(x,y) = 3xy^2 +5x^2 y^2 +B(x) df = 0 ⇒ f(x,y) = C_1 { ((3xy^2 +5x^2 y^2 +A(y) = C_1 (1))),((3xy^2 +5x^2 y^2 +B(x) = C_1 (2))) :} (1)−(2) : ∀x,y, A(y)−B(x) = 0 ⇒ A(y) = B(x) = C_2 Finally f(x,y) = 3xy^2 +5x^2 y^2 +C_2 = C_1 ⇒ y^2 = (C_3 /(x(3+5x)))

$$\left(\mathrm{3}{y}^{\mathrm{2}} +\mathrm{10}{xy}^{\mathrm{2}} \right){dx}+\left(\mathrm{6}{xy}−\mathrm{2}+\mathrm{10}{x}^{\mathrm{2}} {y}\right){dy}\:=\:\mathrm{0} \\ $$$$\mathrm{d}{f}\:=\:\frac{\partial{f}}{\partial{x}}\left({x},{y}\right){dx}+\frac{\partial{f}}{\partial{y}}\left({x},{y}\right){dy}\:=\:\mathrm{0} \\ $$$$ \\ $$$$\mathrm{with}\:: \\ $$$$\frac{\partial{f}}{\partial{x}}\left({x},{y}\right)\:=\:\mathrm{3}{y}^{\mathrm{2}} +\mathrm{10}{xy} \\ $$$$\Rightarrow\:{f}\left({x},{y}\right)\:=\:\mathrm{3}{y}^{\mathrm{2}} {x}+\mathrm{5}{x}^{\mathrm{2}} {y}^{\mathrm{2}} +\mathrm{A}\left({y}\right) \\ $$$$\mathrm{and}\:: \\ $$$$\frac{\partial{f}}{\partial{y}}\left({x},{y}\right)\:=\:\mathrm{6}{xy}−\mathrm{2}+\mathrm{10}{x}^{\mathrm{2}} {y} \\ $$$$\Rightarrow\:{f}\left({x},{y}\right)\:=\:\mathrm{3}{xy}^{\mathrm{2}} +\mathrm{5}{x}^{\mathrm{2}} {y}^{\mathrm{2}} +\mathrm{B}\left({x}\right) \\ $$$$ \\ $$$$\mathrm{d}{f}\:=\:\mathrm{0}\:\Rightarrow\:{f}\left({x},{y}\right)\:=\:\mathrm{C}_{\mathrm{1}} \\ $$$$ \\ $$$$\begin{cases}{\mathrm{3}{xy}^{\mathrm{2}} +\mathrm{5}{x}^{\mathrm{2}} {y}^{\mathrm{2}} +\mathrm{A}\left({y}\right)\:=\:\mathrm{C}_{\mathrm{1}} \:\left(\mathrm{1}\right)}\\{\mathrm{3}{xy}^{\mathrm{2}} +\mathrm{5}{x}^{\mathrm{2}} {y}^{\mathrm{2}} +\mathrm{B}\left({x}\right)\:=\:\mathrm{C}_{\mathrm{1}} \:\left(\mathrm{2}\right)}\end{cases} \\ $$$$\left(\mathrm{1}\right)−\left(\mathrm{2}\right)\::\:\forall{x},{y},\:\mathrm{A}\left({y}\right)−\mathrm{B}\left({x}\right)\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{A}\left({y}\right)\:=\:\mathrm{B}\left({x}\right)\:=\:\mathrm{C}_{\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{Finally}\:{f}\left({x},{y}\right)\:=\:\mathrm{3}{xy}^{\mathrm{2}} +\mathrm{5}{x}^{\mathrm{2}} {y}^{\mathrm{2}} +\mathrm{C}_{\mathrm{2}} \:=\:\mathrm{C}_{\mathrm{1}} \\ $$$$\Rightarrow\:{y}^{\mathrm{2}} \:=\:\frac{\mathrm{C}_{\mathrm{3}} }{{x}\left(\mathrm{3}+\mathrm{5}{x}\right)} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply