Question Number 121552 by I want to learn more last updated on 09/Nov/20

Commented by mr W last updated on 10/Nov/20

$$\mathrm{4}\:{ways}: \\ $$$$\mathrm{8}+\mathrm{7}+\mathrm{2}+\mathrm{1}=\mathrm{6}+\mathrm{5}+\mathrm{4}+\mathrm{3} \\ $$$$\mathrm{8}+\mathrm{6}+\mathrm{3}+\mathrm{1}=\mathrm{7}+\mathrm{5}+\mathrm{4}+\mathrm{2} \\ $$$$\mathrm{8}+\mathrm{5}+\mathrm{4}+\mathrm{1}=\mathrm{7}+\mathrm{6}+\mathrm{3}+\mathrm{2} \\ $$$$\mathrm{8}+\mathrm{5}+\mathrm{3}+\mathrm{2}=\mathrm{7}+\mathrm{6}+\mathrm{4}+\mathrm{1} \\ $$
Commented by I want to learn more last updated on 10/Nov/20

$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$
Commented by I want to learn more last updated on 10/Nov/20

$$\mathrm{I}\:\mathrm{thought}\:\mathrm{we}\:\mathrm{can}\:\mathrm{have}\:\mathrm{a}\:\mathrm{formular}\:\mathrm{before}. \\ $$
Commented by mr W last updated on 10/Nov/20
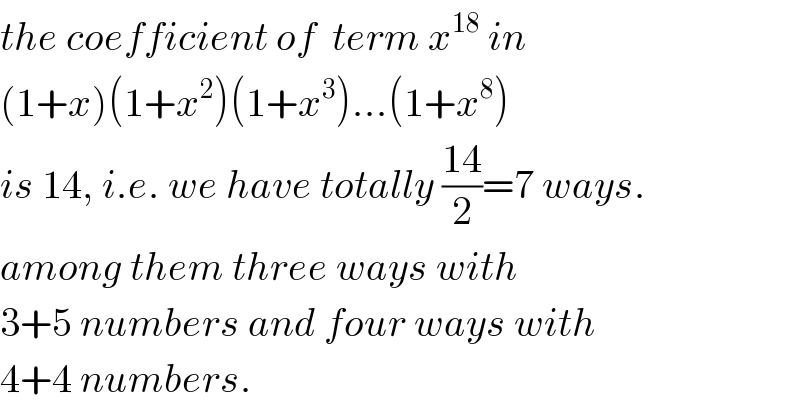
$${the}\:{coefficient}\:{of}\:\:{term}\:{x}^{\mathrm{18}} \:{in} \\ $$$$\left(\mathrm{1}+{x}\right)\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\mathrm{1}+{x}^{\mathrm{3}} \right)…\left(\mathrm{1}+{x}^{\mathrm{8}} \right) \\ $$$${is}\:\mathrm{14},\:{i}.{e}.\:{we}\:{have}\:{totally}\:\frac{\mathrm{14}}{\mathrm{2}}=\mathrm{7}\:{ways}. \\ $$$${among}\:{them}\:{three}\:{ways}\:{with} \\ $$$$\mathrm{3}+\mathrm{5}\:{numbers}\:{and}\:{four}\:{ways}\:{with} \\ $$$$\mathrm{4}+\mathrm{4}\:{numbers}. \\ $$
Commented by I want to learn more last updated on 19/Nov/20
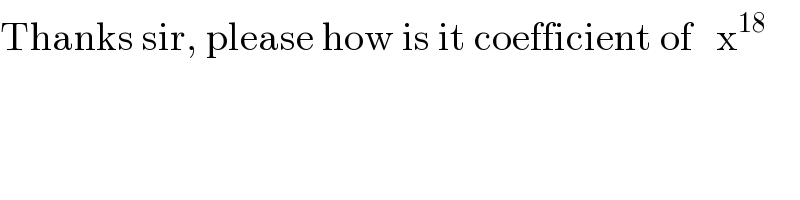
$$\mathrm{Thanks}\:\mathrm{sir},\:\mathrm{please}\:\mathrm{how}\:\mathrm{is}\:\mathrm{it}\:\mathrm{coefficient}\:\mathrm{of}\:\:\:\mathrm{x}^{\mathrm{18}} \\ $$
