Question-121574

Question Number 121574 by oustmuchiya@gmail.com last updated on 09/Nov/20

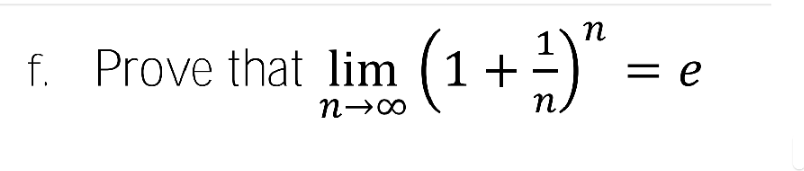
Answered by TANMAY PANACEA last updated on 09/Nov/20

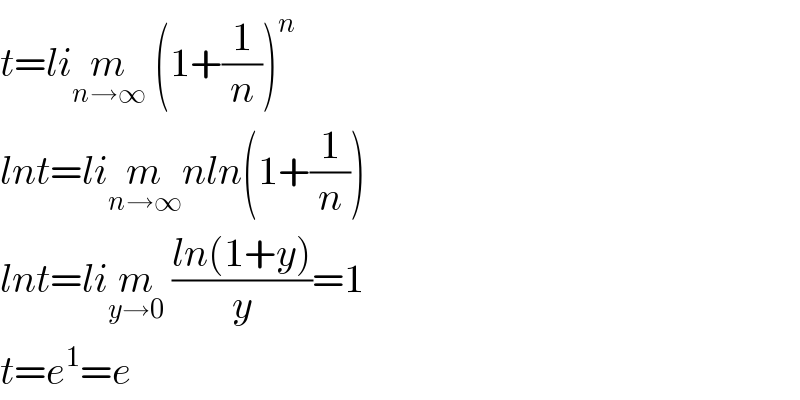
t=lim_(n→∞) (1+(1/n))^n lnt=lim_(n→∞) nln(1+(1/n)) lnt=lim_(y→0) ((ln(1+y))/y)=1 t=e^1 =e

$${t}={li}\underset{{n}\rightarrow\infty} {{m}}\:\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)^{{n}} \\ $$$${lnt}={li}\underset{{n}\rightarrow\infty} {{m}nln}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right) \\ $$$${lnt}={li}\underset{{y}\rightarrow\mathrm{0}} {{m}}\:\frac{{ln}\left(\mathrm{1}+{y}\right)}{{y}}=\mathrm{1} \\ $$$${t}={e}^{\mathrm{1}} ={e} \\ $$

Answered by Dwaipayan Shikari last updated on 09/Nov/20

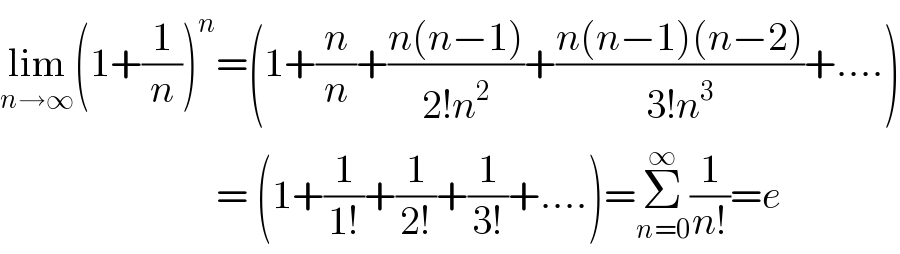
lim_(n→∞) (1+(1/n))^n =(1+(n/n)+((n(n−1))/(2!n^2 ))+((n(n−1)(n−2))/(3!n^3 ))+....) = (1+(1/(1!))+(1/(2!))+(1/(3!))+....)=Σ_(n=0) ^∞ (1/(n!))=e

$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)^{{n}} =\left(\mathrm{1}+\frac{{n}}{{n}}+\frac{{n}\left({n}−\mathrm{1}\right)}{\mathrm{2}!{n}^{\mathrm{2}} }+\frac{{n}\left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right)}{\mathrm{3}!{n}^{\mathrm{3}} }+….\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}!}+\frac{\mathrm{1}}{\mathrm{2}!}+\frac{\mathrm{1}}{\mathrm{3}!}+….\right)=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!}={e} \\ $$

Answered by mathmax by abdo last updated on 09/Nov/20

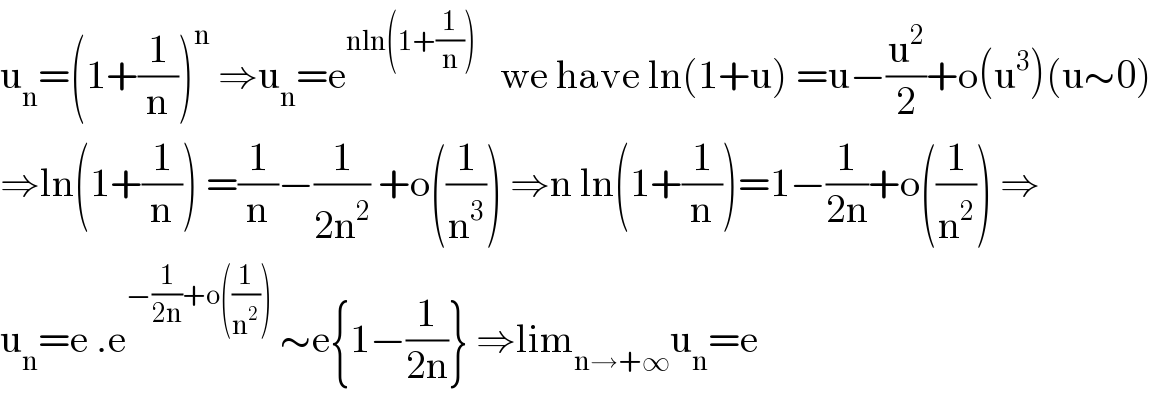
u_n =(1+(1/n))^n ⇒u_n =e^(nln(1+(1/n))) we have ln(1+u) =u−(u^2 /2)+o(u^3 )(u∼0) ⇒ln(1+(1/n)) =(1/n)−(1/(2n^2 )) +o((1/n^3 )) ⇒n ln(1+(1/n))=1−(1/(2n))+o((1/n^2 )) ⇒ u_n =e .e^(−(1/(2n))+o((1/n^2 ))) ∼e{1−(1/(2n))} ⇒lim_(n→+∞) u_n =e

$$\mathrm{u}_{\mathrm{n}} =\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}}\right)^{\mathrm{n}} \:\Rightarrow\mathrm{u}_{\mathrm{n}} =\mathrm{e}^{\mathrm{nln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}}\right)} \:\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{ln}\left(\mathrm{1}+\mathrm{u}\right)\:=\mathrm{u}−\frac{\mathrm{u}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{o}\left(\mathrm{u}^{\mathrm{3}} \right)\left(\mathrm{u}\sim\mathrm{0}\right) \\ $$$$\Rightarrow\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}}\right)\:=\frac{\mathrm{1}}{\mathrm{n}}−\frac{\mathrm{1}}{\mathrm{2n}^{\mathrm{2}} }\:+\mathrm{o}\left(\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{3}} }\right)\:\Rightarrow\mathrm{n}\:\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}}\right)=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2n}}+\mathrm{o}\left(\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\right)\:\Rightarrow \\ $$$$\mathrm{u}_{\mathrm{n}} =\mathrm{e}\:.\mathrm{e}^{−\frac{\mathrm{1}}{\mathrm{2n}}+\mathrm{o}\left(\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\right)} \:\sim\mathrm{e}\left\{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2n}}\right\}\:\Rightarrow\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{u}_{\mathrm{n}} =\mathrm{e} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply