Question-121655

Question Number 121655 by TITA last updated on 10/Nov/20

Commented by Dwaipayan Shikari last updated on 10/Nov/20

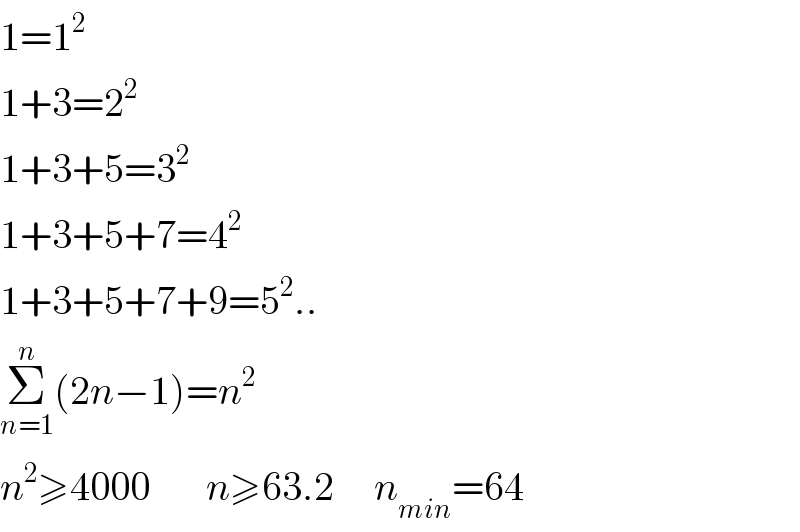
1=1^2 1+3=2^2 1+3+5=3^2 1+3+5+7=4^2 1+3+5+7+9=5^2 .. Σ_(n=1) ^n (2n−1)=n^2 n^2 ≥4000 n≥63.2 n_(min) =64

$$\mathrm{1}=\mathrm{1}^{\mathrm{2}} \\ $$$$\mathrm{1}+\mathrm{3}=\mathrm{2}^{\mathrm{2}} \\ $$$$\mathrm{1}+\mathrm{3}+\mathrm{5}=\mathrm{3}^{\mathrm{2}} \\ $$$$\mathrm{1}+\mathrm{3}+\mathrm{5}+\mathrm{7}=\mathrm{4}^{\mathrm{2}} \\ $$$$\mathrm{1}+\mathrm{3}+\mathrm{5}+\mathrm{7}+\mathrm{9}=\mathrm{5}^{\mathrm{2}} .. \\ $$$$\underset{{n}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\mathrm{2}{n}−\mathrm{1}\right)={n}^{\mathrm{2}} \\ $$$${n}^{\mathrm{2}} \geqslant\mathrm{4000}\:\:\:\:\:\:\:{n}\geqslant\mathrm{63}.\mathrm{2}\:\:\:\:\:{n}_{{min}} =\mathrm{64}\:\: \\ $$

Commented by TITA last updated on 10/Nov/20

$${thanks}\:{sir} \\ $$

Answered by 675480065 last updated on 10/Nov/20

Σ_(k=1 ) ^n (2k−1)=n^2 Use mathematical induction

$$\sum_{\mathrm{k}=\mathrm{1}\:} ^{\mathrm{n}} \left(\mathrm{2k}−\mathrm{1}\right)=\mathrm{n}^{\mathrm{2}} \\ $$$$\mathrm{Use}\:\mathrm{mathematical}\:\mathrm{induction} \\ $$

Answered by TANMAY PANACEA last updated on 11/Nov/20

Direct method S=1+3+5+7..+(2n−1) =(n/2)[2×1+(n−1)×2]→S=(n/2)(2a+(n−1)d] =n^2

$${Direct}\:{method} \\ $$$${S}=\mathrm{1}+\mathrm{3}+\mathrm{5}+\mathrm{7}..+\left(\mathrm{2}{n}−\mathrm{1}\right) \\ $$$$=\frac{{n}}{\mathrm{2}}\left[\mathrm{2}×\mathrm{1}+\left({n}−\mathrm{1}\right)×\mathrm{2}\right]\rightarrow{S}=\frac{{n}}{\mathrm{2}}\left(\mathrm{2}{a}+\left({n}−\mathrm{1}\right){d}\right] \\ $$$$={n}^{\mathrm{2}} \\ $$

Commented by bemath last updated on 11/Nov/20

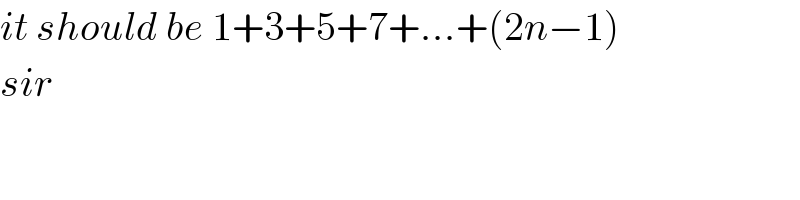
$${it}\:{should}\:{be}\:\mathrm{1}+\mathrm{3}+\mathrm{5}+\mathrm{7}+…+\left(\mathrm{2}{n}−\mathrm{1}\right)\: \\ $$$${sir}\: \\ $$

Commented by TANMAY PANACEA last updated on 11/Nov/20

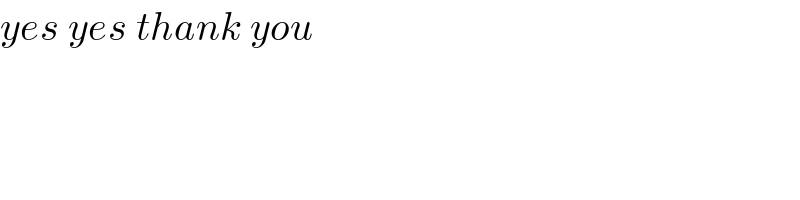
$${yes}\:{yes}\:{thank}\:{you} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply