Question Number 121687 by abdelsalamalmukasabe last updated on 10/Nov/20

Commented by bemath last updated on 11/Nov/20
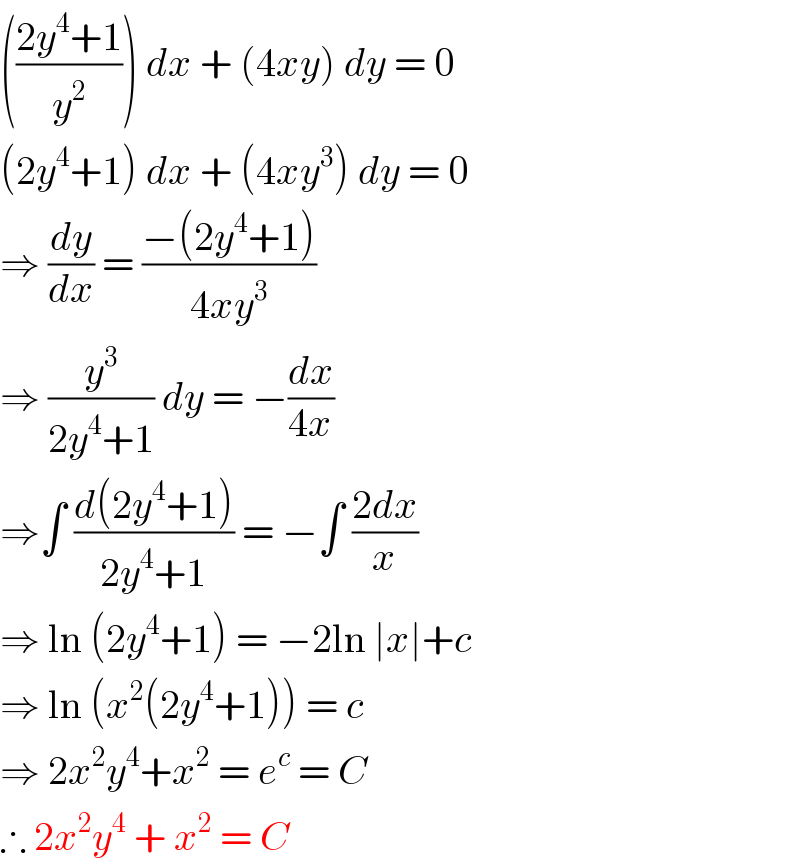
$$\left(\frac{\mathrm{2}{y}^{\mathrm{4}} +\mathrm{1}}{{y}^{\mathrm{2}} }\right)\:{dx}\:+\:\left(\mathrm{4}{xy}\right)\:{dy}\:=\:\mathrm{0} \\ $$$$\left(\mathrm{2}{y}^{\mathrm{4}} +\mathrm{1}\right)\:{dx}\:+\:\left(\mathrm{4}{xy}^{\mathrm{3}} \right)\:{dy}\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\frac{{dy}}{{dx}}\:=\:\frac{−\left(\mathrm{2}{y}^{\mathrm{4}} +\mathrm{1}\right)}{\mathrm{4}{xy}^{\mathrm{3}} } \\ $$$$\Rightarrow\:\frac{{y}^{\mathrm{3}} }{\mathrm{2}{y}^{\mathrm{4}} +\mathrm{1}}\:{dy}\:=\:−\frac{{dx}}{\mathrm{4}{x}} \\ $$$$\Rightarrow\int\:\frac{{d}\left(\mathrm{2}{y}^{\mathrm{4}} +\mathrm{1}\right)}{\mathrm{2}{y}^{\mathrm{4}} +\mathrm{1}}\:=\:−\int\:\frac{\mathrm{2}{dx}}{{x}} \\ $$$$\Rightarrow\:\mathrm{ln}\:\left(\mathrm{2}{y}^{\mathrm{4}} +\mathrm{1}\right)\:=\:−\mathrm{2ln}\:\mid{x}\mid+{c} \\ $$$$\Rightarrow\:\mathrm{ln}\:\left({x}^{\mathrm{2}} \left(\mathrm{2}{y}^{\mathrm{4}} +\mathrm{1}\right)\right)\:=\:{c} \\ $$$$\Rightarrow\:\mathrm{2}{x}^{\mathrm{2}} {y}^{\mathrm{4}} +{x}^{\mathrm{2}} \:=\:{e}^{{c}} \:=\:{C}\: \\ $$$$\therefore\:\mathrm{2}{x}^{\mathrm{2}} {y}^{\mathrm{4}} \:+\:{x}^{\mathrm{2}} \:=\:{C}\: \\ $$
