Question Number 121704 by rs4089 last updated on 11/Nov/20
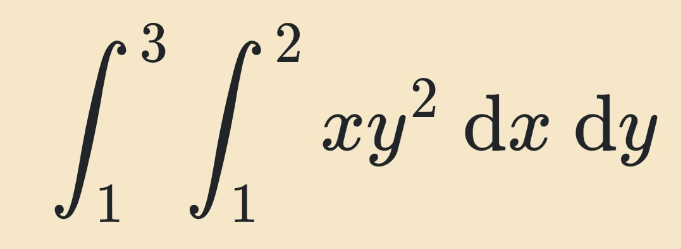
Answered by bemath last updated on 11/Nov/20
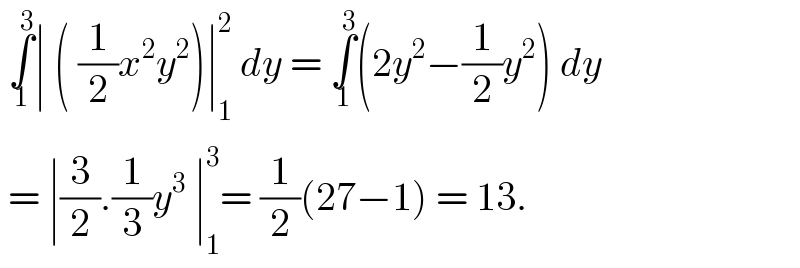
$$\:\underset{\mathrm{1}} {\overset{\mathrm{3}} {\int}}\mid\:\left(\:\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} {y}^{\mathrm{2}} \right)\mid_{\mathrm{1}} ^{\mathrm{2}} \:{dy}\:=\:\underset{\mathrm{1}} {\overset{\mathrm{3}} {\int}}\left(\mathrm{2}{y}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}{y}^{\mathrm{2}} \right)\:{dy} \\ $$$$\:=\:\mid\frac{\mathrm{3}}{\mathrm{2}}.\frac{\mathrm{1}}{\mathrm{3}}{y}^{\mathrm{3}} \:\mid_{\mathrm{1}} ^{\mathrm{3}} =\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{27}−\mathrm{1}\right)\:=\:\mathrm{13}.\: \\ $$
Commented by rs4089 last updated on 11/Nov/20
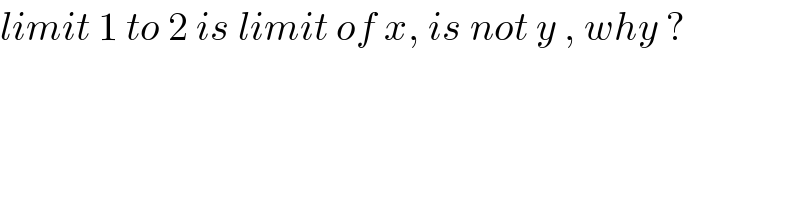
$${limit}\:\mathrm{1}\:{to}\:\mathrm{2}\:{is}\:{limit}\:{of}\:{x},\:{is}\:{not}\:{y}\:,\:{why}\:? \\ $$
Commented by bemath last updated on 11/Nov/20
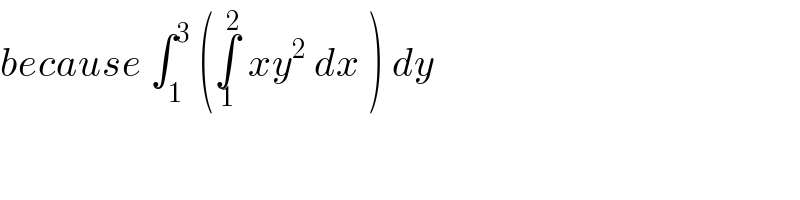
$${because}\:\int_{\mathrm{1}} ^{\mathrm{3}} \:\left(\underset{\mathrm{1}} {\overset{\mathrm{2}} {\int}}\:{xy}^{\mathrm{2}} \:{dx}\:\right)\:{dy}\: \\ $$
