Question Number 121705 by bemath last updated on 11/Nov/20

Answered by MJS_new last updated on 11/Nov/20
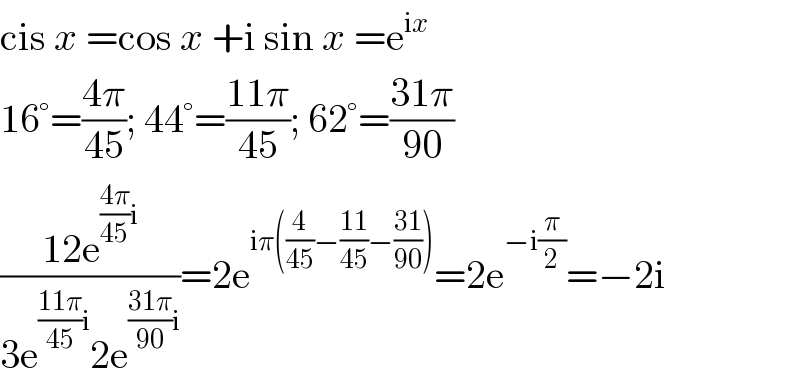
$$\mathrm{cis}\:{x}\:=\mathrm{cos}\:{x}\:+\mathrm{i}\:\mathrm{sin}\:{x}\:=\mathrm{e}^{\mathrm{i}{x}} \\ $$$$\mathrm{16}°=\frac{\mathrm{4}\pi}{\mathrm{45}};\:\mathrm{44}°=\frac{\mathrm{11}\pi}{\mathrm{45}};\:\mathrm{62}°=\frac{\mathrm{31}\pi}{\mathrm{90}} \\ $$$$\frac{\mathrm{12e}^{\frac{\mathrm{4}\pi}{\mathrm{45}}\mathrm{i}} }{\mathrm{3e}^{\frac{\mathrm{11}\pi}{\mathrm{45}}\mathrm{i}} \mathrm{2e}^{\frac{\mathrm{31}\pi}{\mathrm{90}}\mathrm{i}} }=\mathrm{2e}^{\mathrm{i}\pi\left(\frac{\mathrm{4}}{\mathrm{45}}−\frac{\mathrm{11}}{\mathrm{45}}−\frac{\mathrm{31}}{\mathrm{90}}\right)} =\mathrm{2e}^{−\mathrm{i}\frac{\pi}{\mathrm{2}}} =−\mathrm{2i} \\ $$
