Question Number 121723 by oustmuchiya@gmail.com last updated on 11/Nov/20
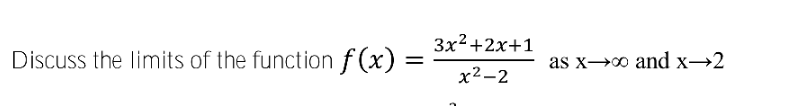
Answered by TANMAY PANACEA last updated on 11/Nov/20
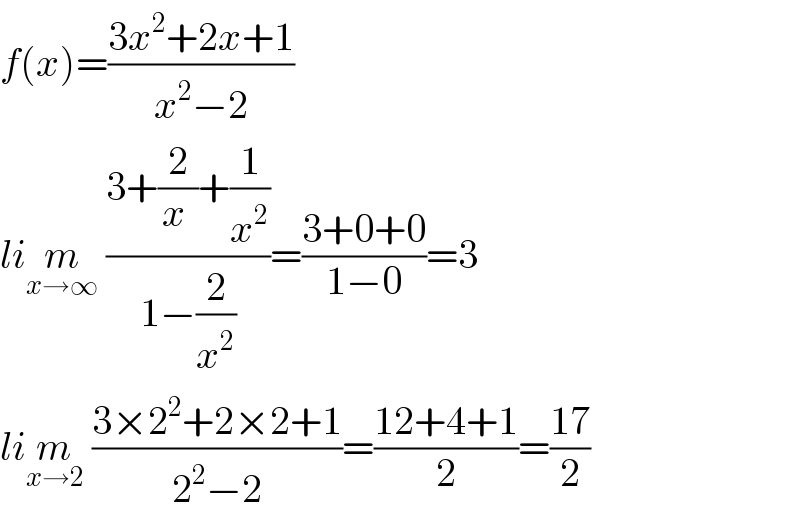
$${f}\left({x}\right)=\frac{\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{1}}{{x}^{\mathrm{2}} −\mathrm{2}} \\ $$$${li}\underset{{x}\rightarrow\infty} {{m}}\:\frac{\mathrm{3}+\frac{\mathrm{2}}{{x}\:}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{\mathrm{1}−\frac{\mathrm{2}}{{x}^{\mathrm{2}} }}=\frac{\mathrm{3}+\mathrm{0}+\mathrm{0}}{\mathrm{1}−\mathrm{0}}=\mathrm{3} \\ $$$${li}\underset{{x}\rightarrow\mathrm{2}} {{m}}\:\frac{\mathrm{3}×\mathrm{2}^{\mathrm{2}} +\mathrm{2}×\mathrm{2}+\mathrm{1}}{\mathrm{2}^{\mathrm{2}} −\mathrm{2}}=\frac{\mathrm{12}+\mathrm{4}+\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{17}}{\mathrm{2}} \\ $$
