Question-121729

Question Number 121729 by oustmuchiya@gmail.com last updated on 11/Nov/20

Answered by bemath last updated on 11/Nov/20

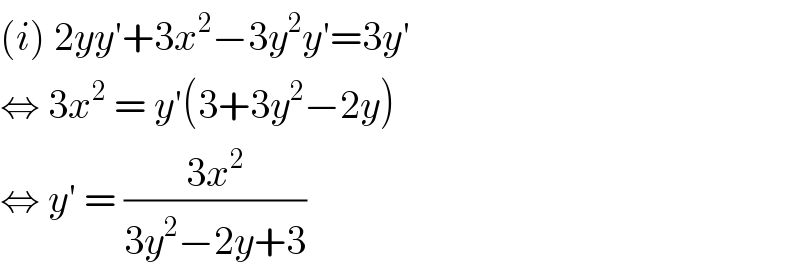
(i) 2yy′+3x^2 −3y^2 y′=3y′ ⇔ 3x^2 = y′(3+3y^2 −2y) ⇔ y′ = ((3x^2 )/(3y^2 −2y+3))

$$\left({i}\right)\:\mathrm{2}{yy}'+\mathrm{3}{x}^{\mathrm{2}} −\mathrm{3}{y}^{\mathrm{2}} {y}'=\mathrm{3}{y}' \\ $$$$\Leftrightarrow\:\mathrm{3}{x}^{\mathrm{2}} \:=\:{y}'\left(\mathrm{3}+\mathrm{3}{y}^{\mathrm{2}} −\mathrm{2}{y}\right) \\ $$$$\Leftrightarrow\:{y}'\:=\:\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{3}{y}^{\mathrm{2}} −\mathrm{2}{y}+\mathrm{3}} \\ $$

Answered by bemath last updated on 11/Nov/20

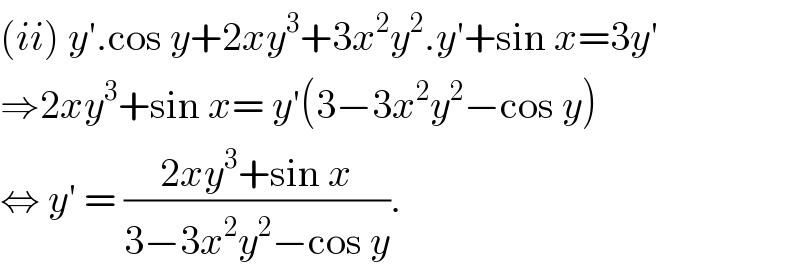
(ii) y′.cos y+2xy^3 +3x^2 y^2 .y′+sin x=3y′ ⇒2xy^3 +sin x= y′(3−3x^2 y^2 −cos y) ⇔ y′ = ((2xy^3 +sin x)/(3−3x^2 y^2 −cos y)).

$$\left({ii}\right)\:{y}'.\mathrm{cos}\:{y}+\mathrm{2}{xy}^{\mathrm{3}} +\mathrm{3}{x}^{\mathrm{2}} {y}^{\mathrm{2}} .{y}'+\mathrm{sin}\:{x}=\mathrm{3}{y}' \\ $$$$\Rightarrow\mathrm{2}{xy}^{\mathrm{3}} +\mathrm{sin}\:{x}=\:{y}'\left(\mathrm{3}−\mathrm{3}{x}^{\mathrm{2}} {y}^{\mathrm{2}} −\mathrm{cos}\:{y}\right) \\ $$$$\Leftrightarrow\:{y}'\:=\:\frac{\mathrm{2}{xy}^{\mathrm{3}} +\mathrm{sin}\:{x}}{\mathrm{3}−\mathrm{3}{x}^{\mathrm{2}} {y}^{\mathrm{2}} −\mathrm{cos}\:{y}}. \\ $$

Answered by bemath last updated on 11/Nov/20

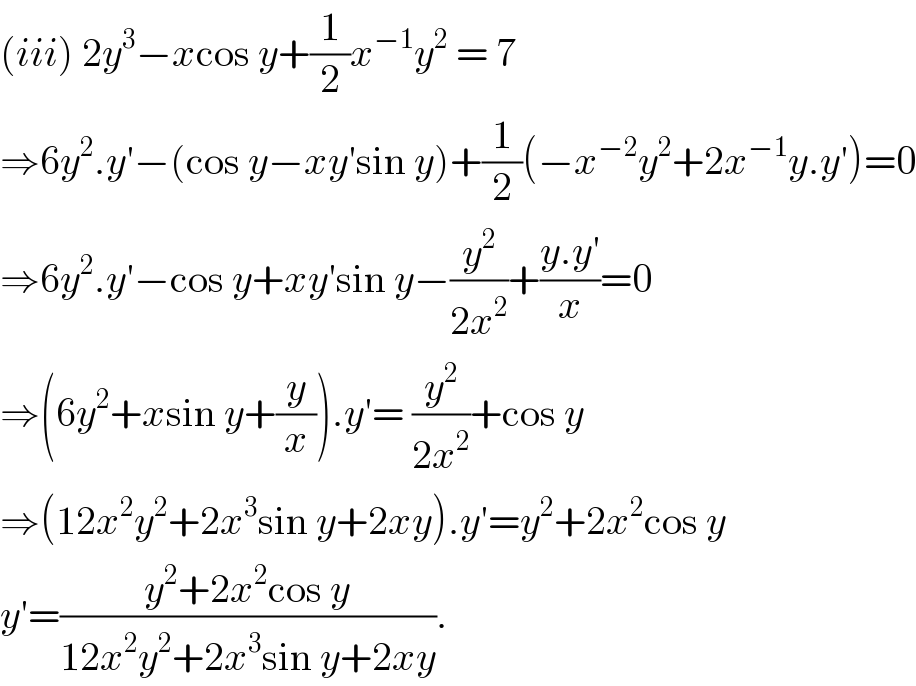
(iii) 2y^3 −xcos y+(1/2)x^(−1) y^2 = 7 ⇒6y^2 .y′−(cos y−xy′sin y)+(1/2)(−x^(−2) y^2 +2x^(−1) y.y′)=0 ⇒6y^2 .y′−cos y+xy′sin y−(y^2 /(2x^2 ))+((y.y′)/x)=0 ⇒(6y^2 +xsin y+(y/x)).y′= (y^2 /(2x^2 ))+cos y ⇒(12x^2 y^2 +2x^3 sin y+2xy).y′=y^2 +2x^2 cos y y′=((y^2 +2x^2 cos y)/(12x^2 y^2 +2x^3 sin y+2xy)).

$$\left({iii}\right)\:\mathrm{2}{y}^{\mathrm{3}} −{x}\mathrm{cos}\:{y}+\frac{\mathrm{1}}{\mathrm{2}}{x}^{−\mathrm{1}} {y}^{\mathrm{2}} \:=\:\mathrm{7} \\ $$$$\Rightarrow\mathrm{6}{y}^{\mathrm{2}} .{y}'−\left(\mathrm{cos}\:{y}−{xy}'\mathrm{sin}\:{y}\right)+\frac{\mathrm{1}}{\mathrm{2}}\left(−{x}^{−\mathrm{2}} {y}^{\mathrm{2}} +\mathrm{2}{x}^{−\mathrm{1}} {y}.{y}'\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{6}{y}^{\mathrm{2}} .{y}'−\mathrm{cos}\:{y}+{xy}'\mathrm{sin}\:{y}−\frac{{y}^{\mathrm{2}} }{\mathrm{2}{x}^{\mathrm{2}} }+\frac{{y}.{y}'}{{x}}=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{6}{y}^{\mathrm{2}} +{x}\mathrm{sin}\:{y}+\frac{{y}}{{x}}\right).{y}'=\:\frac{{y}^{\mathrm{2}} }{\mathrm{2}{x}^{\mathrm{2}} }+\mathrm{cos}\:{y} \\ $$$$\Rightarrow\left(\mathrm{12}{x}^{\mathrm{2}} {y}^{\mathrm{2}} +\mathrm{2}{x}^{\mathrm{3}} \mathrm{sin}\:{y}+\mathrm{2}{xy}\right).{y}'={y}^{\mathrm{2}} +\mathrm{2}{x}^{\mathrm{2}} \mathrm{cos}\:{y} \\ $$$${y}'=\frac{{y}^{\mathrm{2}} +\mathrm{2}{x}^{\mathrm{2}} \mathrm{cos}\:{y}}{\mathrm{12}{x}^{\mathrm{2}} {y}^{\mathrm{2}} +\mathrm{2}{x}^{\mathrm{3}} \mathrm{sin}\:{y}+\mathrm{2}{xy}}.\: \\ $$

Answered by bemath last updated on 11/Nov/20

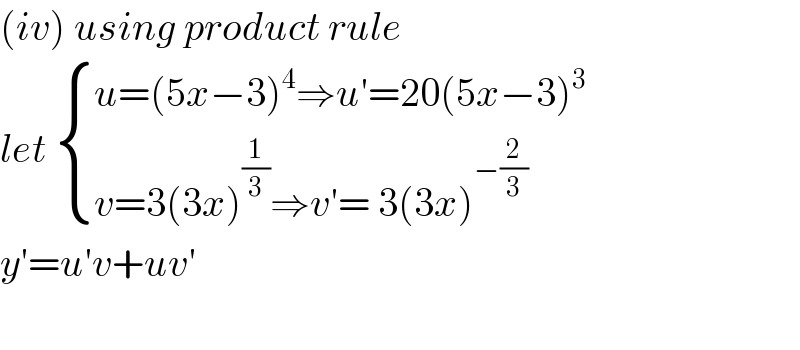
(iv) using product rule let { ((u=(5x−3)^4 ⇒u′=20(5x−3)^3 )),((v=3(3x)^(1/3) ⇒v′= 3(3x)^(−(2/3)) )) :} y′=u′v+uv′

$$\left({iv}\right)\:{using}\:{product}\:{rule} \\ $$$${let}\:\begin{cases}{{u}=\left(\mathrm{5}{x}−\mathrm{3}\right)^{\mathrm{4}} \Rightarrow{u}'=\mathrm{20}\left(\mathrm{5}{x}−\mathrm{3}\right)^{\mathrm{3}} }\\{{v}=\mathrm{3}\left(\mathrm{3}{x}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \Rightarrow{v}'=\:\mathrm{3}\left(\mathrm{3}{x}\right)^{−\frac{\mathrm{2}}{\mathrm{3}}} }\end{cases} \\ $$$${y}'={u}'{v}+{uv}' \\ $$$$ \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply