Menu Close

Question-121754

Tinku Tara 0 Comments
Pin




Question Number 121754 by bemath last updated on 11/Nov/20
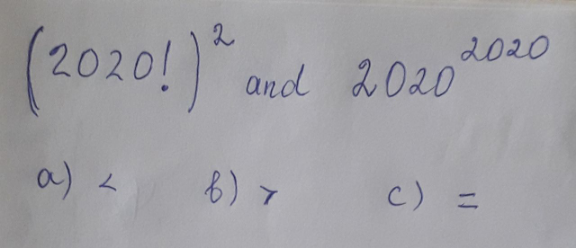
Answered by liberty last updated on 11/Nov/20
let y = (2020!)^2 ⇒ln y = 2(ln 2020+ln 2019+ln 2018+...+ln 1) let x = 2020^(2020) ⇒ln x = 2020 ln (2020) consider ln x−ln y = 2020ln (2020)−2(ln 2020+ln 2019+...+ln 1) ln x−ln y = 2018.ln 2020−2ln (2019!)>0 so ln x > ln y ⇒ x > y
$$\mathrm{let}\:\mathrm{y}\:=\:\left(\mathrm{2020}!\right)^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{ln}\:\mathrm{y}\:=\:\mathrm{2}\left(\mathrm{ln}\:\mathrm{2020}+\mathrm{ln}\:\mathrm{2019}+\mathrm{ln}\:\mathrm{2018}+…+\mathrm{ln}\:\mathrm{1}\right) \\ $$$$\mathrm{let}\:\mathrm{x}\:=\:\mathrm{2020}^{\mathrm{2020}} \\ $$$$\Rightarrow\mathrm{ln}\:\mathrm{x}\:=\:\mathrm{2020}\:\mathrm{ln}\:\left(\mathrm{2020}\right)\: \\ $$$$ \\ $$$$\mathrm{consider}\:\mathrm{ln}\:\mathrm{x}−\mathrm{ln}\:\mathrm{y}\:=\:\mathrm{2020ln}\:\left(\mathrm{2020}\right)−\mathrm{2}\left(\mathrm{ln}\:\mathrm{2020}+\mathrm{ln}\:\mathrm{2019}+…+\mathrm{ln}\:\mathrm{1}\right) \\ $$$$\mathrm{ln}\:\mathrm{x}−\mathrm{ln}\:\mathrm{y}\:=\:\mathrm{2018}.\mathrm{ln}\:\mathrm{2020}−\mathrm{2ln}\:\left(\mathrm{2019}!\right)>\mathrm{0} \\ $$$$\mathrm{so}\:\mathrm{ln}\:\mathrm{x}\:>\:\mathrm{ln}\:\mathrm{y}\:\Rightarrow\:\mathrm{x}\:>\:\mathrm{y}\: \\ $$$$ \\ $$
Commented by MJS_new last updated on 11/Nov/20
(1!)^2 =1 ^ 1^1 =1 (2!)^2 =4 2^2 =4 (3!)^2 =36 3^3 =27 (4!)^2 =576 ^ 4^4 =256 ... (n!)^2 ≥n^n ∀n∈N^★ using Stirling′s Approximation lim_(n→∞) (n!− (n^n /e^n )(√(2πn))) =0 and n!>(n^n /e^n )(√(2πn)) (n!)^2 <>n^n (n^(2n) /e^(2n) )2πn<>n^n n^(2n) 2πn<>n^n e^(2n) both sides >0 2nln n +ln n +ln 2π <> nln n +2n (n+1)ln n <> 2n−ln 2π ln n <> 2−((2+ln 2π)/(n+1)) obviously ln n > 2 ∀ n>e^2 [ln n = 2−((2+ln 2π)/(n+1)) ⇒ n≈2.34940] 2020>e^2 ⇒ (2020!)^2 >((2020^(4040) )/e^(4040) )4040π>2020^(2020)
$$\left(\mathrm{1}!\right)^{\mathrm{2}} =\mathrm{1}\:\:\:\:\:^{\:} \:\:\:\mathrm{1}^{\mathrm{1}} =\mathrm{1} \\ $$$$\left(\mathrm{2}!\right)^{\mathrm{2}} =\mathrm{4}\:\:\:\:\:\:\:\:\:\mathrm{2}^{\mathrm{2}} =\mathrm{4} \\ $$$$\left(\mathrm{3}!\right)^{\mathrm{2}} =\mathrm{36}\:\:\:\:\:\:\:\mathrm{3}^{\mathrm{3}} =\mathrm{27} \\ $$$$\left(\mathrm{4}!\right)^{\mathrm{2}} =\mathrm{576}\:\:\:^{\:} \:\mathrm{4}^{\mathrm{4}} =\mathrm{256} \\ $$$$… \\ $$$$\left({n}!\right)^{\mathrm{2}} \geqslant{n}^{{n}} \:\forall{n}\in\mathbb{N}^{\bigstar} \\ $$$$ \\ $$$$\mathrm{using}\:\mathrm{Stirling}'\mathrm{s}\:\mathrm{Approximation} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left({n}!−\:\frac{{n}^{{n}} }{\mathrm{e}^{{n}} }\sqrt{\mathrm{2}\pi{n}}\right)\:=\mathrm{0}\:\mathrm{and}\:{n}!>\frac{{n}^{{n}} }{\mathrm{e}^{{n}} }\sqrt{\mathrm{2}\pi{n}} \\ $$$$\left({n}!\right)^{\mathrm{2}} <>{n}^{{n}} \\ $$$$\frac{{n}^{\mathrm{2}{n}} }{\mathrm{e}^{\mathrm{2}{n}} }\mathrm{2}\pi{n}<>{n}^{{n}} \\ $$$${n}^{\mathrm{2}{n}} \mathrm{2}\pi{n}<>{n}^{{n}} \mathrm{e}^{\mathrm{2}{n}} \\ $$$$\mathrm{both}\:\mathrm{sides}\:>\mathrm{0} \\ $$$$\mathrm{2}{n}\mathrm{ln}\:{n}\:+\mathrm{ln}\:{n}\:+\mathrm{ln}\:\mathrm{2}\pi\:<>\:{n}\mathrm{ln}\:{n}\:+\mathrm{2}{n} \\ $$$$\left({n}+\mathrm{1}\right)\mathrm{ln}\:{n}\:<>\:\mathrm{2}{n}−\mathrm{ln}\:\mathrm{2}\pi \\ $$$$\mathrm{ln}\:{n}\:<>\:\mathrm{2}−\frac{\mathrm{2}+\mathrm{ln}\:\mathrm{2}\pi}{{n}+\mathrm{1}} \\ $$$$\mathrm{obviously}\:\mathrm{ln}\:{n}\:>\:\mathrm{2}\:\forall\:{n}>\mathrm{e}^{\mathrm{2}} \\ $$$$\left[\mathrm{ln}\:{n}\:=\:\mathrm{2}−\frac{\mathrm{2}+\mathrm{ln}\:\mathrm{2}\pi}{{n}+\mathrm{1}}\:\Rightarrow\:{n}\approx\mathrm{2}.\mathrm{34940}\right] \\ $$$$ \\ $$$$\mathrm{2020}>\mathrm{e}^{\mathrm{2}} \:\Rightarrow\:\left(\mathrm{2020}!\right)^{\mathrm{2}} >\frac{\mathrm{2020}^{\mathrm{4040}} }{\mathrm{e}^{\mathrm{4040}} }\mathrm{4040}\pi>\mathrm{2020}^{\mathrm{2020}} \\ $$
Answered by TANMAY PANACEA last updated on 11/Nov/20
(n!)^2 =A B=n^n n!=n(n−1)(n−2)(n−3)..(n−r+1)..3×2×1⇚r_(th) term=(n−r+1)=T_r n!=1×2×3×...×r×(n−2)(n−1)n⇚ r_(th) term=r=t_r (n!)^2 =(n×1)×{(n−1)×2}{(n−2)×3...{(n−r+1)r}...{2×(n−1)}{1×n} now look r_(th) term of (n!)^2 is (n−r+1)r value of (T_r t_r −n) is T_r t_r −n (n−r+1)r−n =nr−r^2 +r−n =r(n−r)−1(n−r) =(n−r)(r−1) is greater than zero when n>r>1 so T_r t_r >n T_1 t_1 >n T_2 t_2 >n T_3 t_3 >n ... .... T_n t_n >n multiply both side (T_1 t_1 )(T_2 t_2 )...(T_n t_n )>n^n (n!)^2 >n^n so (2020!)^2 >(2020)^(2020)
$$\left({n}!\right)^{\mathrm{2}} ={A}\:\:\:{B}={n}^{{n}} \\ $$$${n}!={n}\left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right)\left({n}−\mathrm{3}\right)..\left({n}−{r}+\mathrm{1}\right)..\mathrm{3}×\mathrm{2}×\mathrm{1}\Lleftarrow{r}_{{th}} {term}=\left({n}−{r}+\mathrm{1}\right)={T}_{{r}} \\ $$$${n}!=\mathrm{1}×\mathrm{2}×\mathrm{3}×…×{r}×\left({n}−\mathrm{2}\right)\left({n}−\mathrm{1}\right){n}\Lleftarrow\:{r}_{{th}} {term}={r}={t}_{{r}} \\ $$$$\left({n}!\right)^{\mathrm{2}} =\left({n}×\mathrm{1}\right)×\left\{\left({n}−\mathrm{1}\right)×\mathrm{2}\right\}\left\{\left({n}−\mathrm{2}\right)×\mathrm{3}…\left\{\left({n}−{r}+\mathrm{1}\right){r}\right\}…\left\{\mathrm{2}×\left({n}−\mathrm{1}\right)\right\}\left\{\mathrm{1}×{n}\right\}\right. \\ $$$$\:{now}\:{look}\:{r}_{{th}} \:{term}\:{of}\:\left({n}!\right)^{\mathrm{2}} \:{is}\:\left({n}−{r}+\mathrm{1}\right){r} \\ $$$${value}\:{of}\:\left({T}_{{r}} {t}_{{r}} −{n}\right)\:{is} \\ $$$${T}_{{r}} {t}_{{r}} −{n} \\ $$$$\left({n}−{r}+\mathrm{1}\right){r}−{n} \\ $$$$={nr}−{r}^{\mathrm{2}} +{r}−{n} \\ $$$$={r}\left({n}−{r}\right)−\mathrm{1}\left({n}−{r}\right) \\ $$$$=\left({n}−{r}\right)\left({r}−\mathrm{1}\right)\:{is}\:{greater}\:{than}\:{zero}\:{when}\:\:{n}>{r}>\mathrm{1} \\ $$$${so}\:{T}_{{r}} {t}_{{r}} >{n} \\ $$$${T}_{\mathrm{1}} {t}_{\mathrm{1}} >{n} \\ $$$${T}_{\mathrm{2}} {t}_{\mathrm{2}} >{n} \\ $$$${T}_{\mathrm{3}} {t}_{\mathrm{3}} >{n} \\ $$$$… \\ $$$$…. \\ $$$${T}_{{n}} {t}_{{n}} >{n} \\ $$$${multiply}\:{both}\:{side} \\ $$$$\left({T}_{\mathrm{1}} {t}_{\mathrm{1}} \right)\left({T}_{\mathrm{2}} {t}_{\mathrm{2}} \right)…\left({T}_{{n}} {t}_{{n}} \right)>{n}^{{n}} \\ $$$$\left({n}!\right)^{\mathrm{2}} >{n}^{{n}} \\ $$$$\boldsymbol{{so}}\:\left(\mathrm{2020}!\right)^{\mathrm{2}} >\left(\mathrm{2020}\right)^{\mathrm{2020}} \\ $$$$ \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *