Question Number 121887 by oustmuchiya@gmail.com last updated on 12/Nov/20
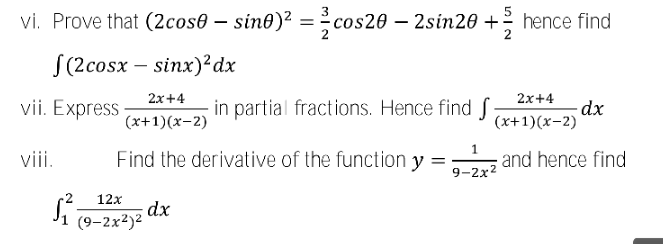
Commented by liberty last updated on 12/Nov/20
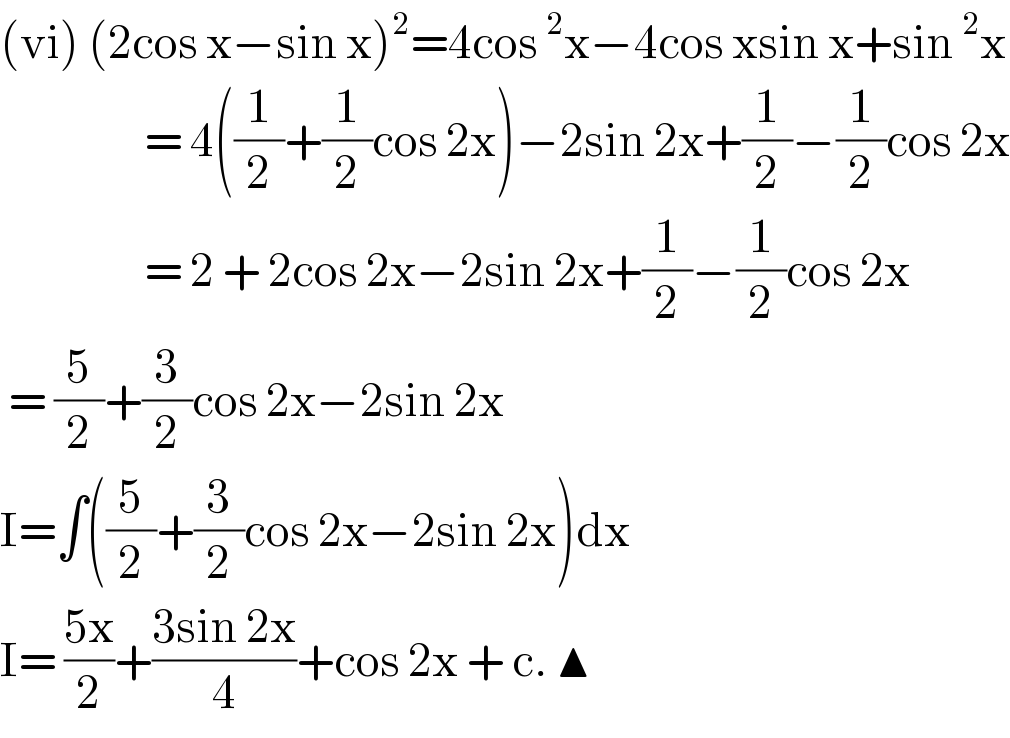
$$\left(\mathrm{vi}\right)\:\left(\mathrm{2cos}\:\mathrm{x}−\mathrm{sin}\:\mathrm{x}\right)^{\mathrm{2}} =\mathrm{4cos}\:^{\mathrm{2}} \mathrm{x}−\mathrm{4cos}\:\mathrm{xsin}\:\mathrm{x}+\mathrm{sin}\:^{\mathrm{2}} \mathrm{x} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{4}\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\mathrm{2x}\right)−\mathrm{2sin}\:\mathrm{2x}+\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\mathrm{2x} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{2}\:+\:\mathrm{2cos}\:\mathrm{2x}−\mathrm{2sin}\:\mathrm{2x}+\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\mathrm{2x} \\ $$$$\:=\:\frac{\mathrm{5}}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{2}}\mathrm{cos}\:\mathrm{2x}−\mathrm{2sin}\:\mathrm{2x} \\ $$$$\mathrm{I}=\int\left(\frac{\mathrm{5}}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{2}}\mathrm{cos}\:\mathrm{2x}−\mathrm{2sin}\:\mathrm{2x}\right)\mathrm{dx} \\ $$$$\mathrm{I}=\:\frac{\mathrm{5x}}{\mathrm{2}}+\frac{\mathrm{3sin}\:\mathrm{2x}}{\mathrm{4}}+\mathrm{cos}\:\mathrm{2x}\:+\:\mathrm{c}.\:\blacktriangle \\ $$
Commented by bemath last updated on 12/Nov/20
![(vii) ((2x+4)/((x+1)(x−2))) = (p/(x+1)) + (q/(x−2)) → { ((p = [((2x+4)/(x−2)) ]_(x = −1) = −(2/3))),((q = [ ((2x+4)/(x+1)) ]_(x = 2) = (8/3))) :} I = ∫ (8/(3(x−2))) − (2/(3(x+1))) dx I = (8/3) ln ∣x−2∣ − (2/3)ln ∣x+1∣ + c I = (2/3)ln((((x−2)^4 )/(∣x+1∣)) ) + c . ⧫](https://www.tinkutara.com/question/Q121895.png)
$$\left({vii}\right)\:\frac{\mathrm{2}{x}+\mathrm{4}}{\left({x}+\mathrm{1}\right)\left({x}−\mathrm{2}\right)}\:=\:\frac{{p}}{{x}+\mathrm{1}}\:+\:\frac{{q}}{{x}−\mathrm{2}} \\ $$$$\rightarrow\begin{cases}{{p}\:=\:\left[\frac{\mathrm{2}{x}+\mathrm{4}}{{x}−\mathrm{2}}\:\right]_{{x}\:=\:−\mathrm{1}} =\:−\frac{\mathrm{2}}{\mathrm{3}}}\\{{q}\:=\:\left[\:\frac{\mathrm{2}{x}+\mathrm{4}}{{x}+\mathrm{1}}\:\right]_{{x}\:=\:\mathrm{2}} =\:\frac{\mathrm{8}}{\mathrm{3}}}\end{cases} \\ $$$${I}\:=\:\int\:\frac{\mathrm{8}}{\mathrm{3}\left({x}−\mathrm{2}\right)}\:−\:\frac{\mathrm{2}}{\mathrm{3}\left({x}+\mathrm{1}\right)}\:{dx}\: \\ $$$${I}\:=\:\frac{\mathrm{8}}{\mathrm{3}}\:\mathrm{ln}\:\mid{x}−\mathrm{2}\mid\:−\:\frac{\mathrm{2}}{\mathrm{3}}\mathrm{ln}\:\mid{x}+\mathrm{1}\mid\:+\:{c} \\ $$$${I}\:=\:\frac{\mathrm{2}}{\mathrm{3}}\mathrm{ln}\left(\frac{\left({x}−\mathrm{2}\right)^{\mathrm{4}} }{\mid{x}+\mathrm{1}\mid}\:\right)\:+\:{c}\:.\:\blacklozenge\: \\ $$
Answered by Dwaipayan Shikari last updated on 12/Nov/20
![∫_1 ^2 ((12x)/((9−2x^2 )^2 ))dx (9−2x^2 =t⇒−4x=(dt/dx) =3∫_1 ^7 (dt/t^2 )=[−(3/t)]_1 ^7 =−(3/7)+3=((18)/7)](https://www.tinkutara.com/question/Q121927.png)
$$\int_{\mathrm{1}} ^{\mathrm{2}} \frac{\mathrm{12}{x}}{\left(\mathrm{9}−\mathrm{2}{x}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx}\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{9}−\mathrm{2}{x}^{\mathrm{2}} ={t}\Rightarrow−\mathrm{4}{x}=\frac{{dt}}{{dx}}\right. \\ $$$$=\mathrm{3}\int_{\mathrm{1}} ^{\mathrm{7}} \frac{{dt}}{{t}^{\mathrm{2}} }=\left[−\frac{\mathrm{3}}{{t}}\right]_{\mathrm{1}} ^{\mathrm{7}} \: \\ $$$$=−\frac{\mathrm{3}}{\mathrm{7}}+\mathrm{3}=\frac{\mathrm{18}}{\mathrm{7}} \\ $$
Answered by mathmax by abdo last updated on 12/Nov/20
![y=(1/(9−2x^2 )) ⇒y^′ =−((−4x)/((9−2x^2 )^2 )) =((4x)/((9−2x^2 )^2 )) ⇒ ∫_1 ^2 ((12xdx)/((9−2x^2 )^2 )) =3 ∫_1 ^2 ((4x)/((9−2x^2 )^2 ))dx =3[(1/(9−2x^2 ))]_1 ^2 =3{1−(1/7)} =3.(6/7) =((18)/7)](https://www.tinkutara.com/question/Q121945.png)
$$\mathrm{y}=\frac{\mathrm{1}}{\mathrm{9}−\mathrm{2x}^{\mathrm{2}} }\:\Rightarrow\mathrm{y}^{'} \:=−\frac{−\mathrm{4x}}{\left(\mathrm{9}−\mathrm{2x}^{\mathrm{2}} \right)^{\mathrm{2}} }\:=\frac{\mathrm{4x}}{\left(\mathrm{9}−\mathrm{2x}^{\mathrm{2}} \right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\int_{\mathrm{1}} ^{\mathrm{2}} \:\frac{\mathrm{12xdx}}{\left(\mathrm{9}−\mathrm{2x}^{\mathrm{2}} \right)^{\mathrm{2}} }\:=\mathrm{3}\:\int_{\mathrm{1}} ^{\mathrm{2}} \:\frac{\mathrm{4x}}{\left(\mathrm{9}−\mathrm{2x}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dx}\:=\mathrm{3}\left[\frac{\mathrm{1}}{\mathrm{9}−\mathrm{2x}^{\mathrm{2}} }\right]_{\mathrm{1}} ^{\mathrm{2}} \:=\mathrm{3}\left\{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{7}}\right\}\:=\mathrm{3}.\frac{\mathrm{6}}{\mathrm{7}} \\ $$$$=\frac{\mathrm{18}}{\mathrm{7}} \\ $$
