Question-121890

Question Number 121890 by oustmuchiya@gmail.com last updated on 12/Nov/20

Commented by liberty last updated on 12/Nov/20

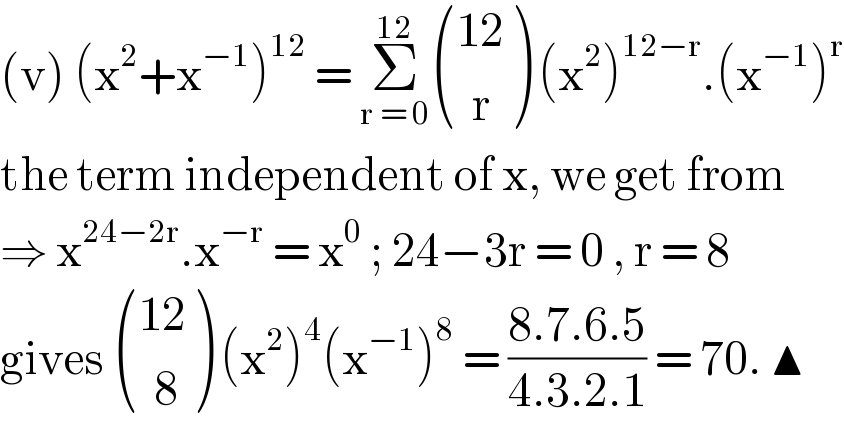
(v) (x^2 +x^(−1) )^(12) = Σ_(r = 0) ^(12) (((12)),(( r)) ) (x^2 )^(12−r) .(x^(−1) )^r the term independent of x, we get from ⇒ x^(24−2r) .x^(−r) = x^0 ; 24−3r = 0 , r = 8 gives (((12)),(( 8)) ) (x^2 )^4 (x^(−1) )^8 = ((8.7.6.5)/(4.3.2.1)) = 70. ▲

$$\left(\mathrm{v}\right)\:\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}^{−\mathrm{1}} \right)^{\mathrm{12}} \:=\:\underset{\mathrm{r}\:=\:\mathrm{0}} {\overset{\mathrm{12}} {\sum}}\begin{pmatrix}{\mathrm{12}}\\{\:\:\mathrm{r}}\end{pmatrix}\:\left(\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{12}−\mathrm{r}} .\left(\mathrm{x}^{−\mathrm{1}} \right)^{\mathrm{r}} \\ $$$$\mathrm{the}\:\mathrm{term}\:\mathrm{independent}\:\mathrm{of}\:\mathrm{x},\:\mathrm{we}\:\mathrm{get}\:\mathrm{from} \\ $$$$\Rightarrow\:\mathrm{x}^{\mathrm{24}−\mathrm{2r}} .\mathrm{x}^{−\mathrm{r}} \:=\:\mathrm{x}^{\mathrm{0}} \:;\:\mathrm{24}−\mathrm{3r}\:=\:\mathrm{0}\:,\:\mathrm{r}\:=\:\mathrm{8} \\ $$$$\mathrm{gives}\:\begin{pmatrix}{\mathrm{12}}\\{\:\:\mathrm{8}}\end{pmatrix}\:\left(\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{4}} \left(\mathrm{x}^{−\mathrm{1}} \right)^{\mathrm{8}} \:=\:\frac{\mathrm{8}.\mathrm{7}.\mathrm{6}.\mathrm{5}}{\mathrm{4}.\mathrm{3}.\mathrm{2}.\mathrm{1}}\:=\:\mathrm{70}.\:\blacktriangle \\ $$

Answered by bemath last updated on 12/Nov/20

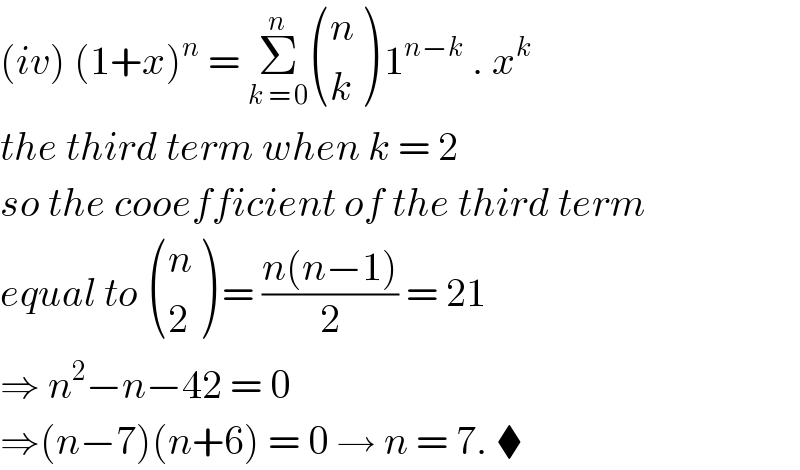
(iv) (1+x)^n = Σ_(k = 0) ^n ((n),(k) ) 1^(n−k) . x^k the third term when k = 2 so the cooefficient of the third term equal to ((n),(2) ) = ((n(n−1))/2) = 21 ⇒ n^2 −n−42 = 0 ⇒(n−7)(n+6) = 0 → n = 7. ⧫

$$\left({iv}\right)\:\left(\mathrm{1}+{x}\right)^{{n}} \:=\:\underset{{k}\:=\:\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}\:\mathrm{1}^{{n}−{k}} \:.\:{x}^{{k}} \: \\ $$$${the}\:{third}\:{term}\:{when}\:{k}\:=\:\mathrm{2}\: \\ $$$${so}\:{the}\:{cooefficient}\:{of}\:{the}\:{third}\:{term} \\ $$$${equal}\:{to}\:\begin{pmatrix}{{n}}\\{\mathrm{2}}\end{pmatrix}\:=\:\frac{{n}\left({n}−\mathrm{1}\right)}{\mathrm{2}}\:=\:\mathrm{21} \\ $$$$\Rightarrow\:{n}^{\mathrm{2}} −{n}−\mathrm{42}\:=\:\mathrm{0}\: \\ $$$$\Rightarrow\left({n}−\mathrm{7}\right)\left({n}+\mathrm{6}\right)\:=\:\mathrm{0}\:\rightarrow\:{n}\:=\:\mathrm{7}.\:\blacklozenge \\ $$

Answered by TANMAY PANACEA last updated on 12/Nov/20

i)(1−(x/2))^5 =1−5C_1 ((x/2))+5C_2 ((x/2))^2 −5C_3 ((x/2))^3 +5C_4 ((x/2))^4 −((x/2))^5 ii)(1+(x/2))^5 +(1−(x/2))^5 ⇚note odd terms cancelled =2[1+5C_2 ((x/2))^2 +5C_4 ((x/2))^4 ] iii)put x=0.1to find (1.05)^5 +(0.95)^4

$$\left.{i}\right)\left(\mathrm{1}−\frac{{x}}{\mathrm{2}}\right)^{\mathrm{5}} \\ $$$$=\mathrm{1}−\mathrm{5}{C}_{\mathrm{1}} \left(\frac{{x}}{\mathrm{2}}\right)+\mathrm{5}{C}_{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)^{\mathrm{2}} −\mathrm{5}{C}_{\mathrm{3}} \left(\frac{{x}}{\mathrm{2}}\right)^{\mathrm{3}} +\mathrm{5}{C}_{\mathrm{4}} \left(\frac{{x}}{\mathrm{2}}\right)^{\mathrm{4}} −\left(\frac{{x}}{\mathrm{2}}\right)^{\mathrm{5}} \\ $$$$\left.{ii}\right)\left(\mathrm{1}+\frac{{x}}{\mathrm{2}}\right)^{\mathrm{5}} +\left(\mathrm{1}−\frac{{x}}{\mathrm{2}}\right)^{\mathrm{5}} \Lleftarrow{note}\:{odd}\:{terms}\:{cancelled} \\ $$$$=\mathrm{2}\left[\mathrm{1}+\mathrm{5}{C}_{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{5}{C}_{\mathrm{4}} \left(\frac{{x}}{\mathrm{2}}\right)^{\mathrm{4}} \right] \\ $$$$\left.{iii}\right){put}\:{x}=\mathrm{0}.\mathrm{1}{to}\:{find}\:\left(\mathrm{1}.\mathrm{05}\right)^{\mathrm{5}} +\left(\mathrm{0}.\mathrm{95}\right)^{\mathrm{4}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply