Question Number 122056 by I want to learn more last updated on 13/Nov/20

Commented by 676597498 last updated on 13/Nov/20

$$\mathrm{your}\:\mathrm{posting}\:\mathrm{iymc}\:\mathrm{questions} \\ $$$$\mathrm{you}\:\mathrm{will}\:\mathrm{be}\:\mathrm{disqualified} \\ $$$$\mathrm{i}\:\mathrm{have}\:\mathrm{no}\:\mathrm{option}\:\mathrm{but}\:\mathrm{to}\:\mathrm{report} \\ $$
Commented by 676597498 last updated on 13/Nov/20

$$\mathrm{This}\:\mathrm{guy}\:\mathrm{is}\:\mathrm{posting}\:\mathrm{questions} \\ $$$$\mathrm{of}\:\mathrm{this}\:\mathrm{competition}\:\left(\mathrm{iymc}.\mathrm{info}\right) \\ $$
Answered by mathmax by abdo last updated on 14/Nov/20
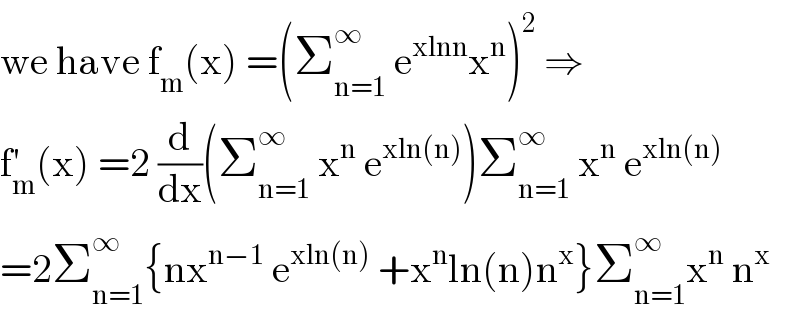
$$\mathrm{we}\:\mathrm{have}\:\mathrm{f}_{\mathrm{m}} \left(\mathrm{x}\right)\:=\left(\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{e}^{\mathrm{xlnn}} \mathrm{x}^{\mathrm{n}} \right)^{\mathrm{2}} \:\Rightarrow \\ $$$$\mathrm{f}_{\mathrm{m}} ^{'} \left(\mathrm{x}\right)\:=\mathrm{2}\:\frac{\mathrm{d}}{\mathrm{dx}}\left(\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{x}^{\mathrm{n}} \:\mathrm{e}^{\mathrm{xln}\left(\mathrm{n}\right)} \right)\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{x}^{\mathrm{n}} \:\mathrm{e}^{\mathrm{xln}\left(\mathrm{n}\right)} \\ $$$$=\mathrm{2}\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \left\{\mathrm{nx}^{\mathrm{n}−\mathrm{1}} \:\mathrm{e}^{\mathrm{xln}\left(\mathrm{n}\right)} \:+\mathrm{x}^{\mathrm{n}} \mathrm{ln}\left(\mathrm{n}\right)\mathrm{n}^{\mathrm{x}} \right\}\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \mathrm{x}^{\mathrm{n}} \:\mathrm{n}^{\mathrm{x}} \\ $$
Commented by I want to learn more last updated on 14/Nov/20
$$\mathrm{Thanks}\:\mathrm{sir},\:\mathrm{i}\:\mathrm{appreciate}. \\ $$
Commented by mathmax by abdo last updated on 15/Nov/20

$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome} \\ $$
