Menu Close

Question-122076

Tinku Tara 0 Comments
Pin




Question Number 122076 by peter frank last updated on 14/Nov/20
Answered by MJS_new last updated on 14/Nov/20
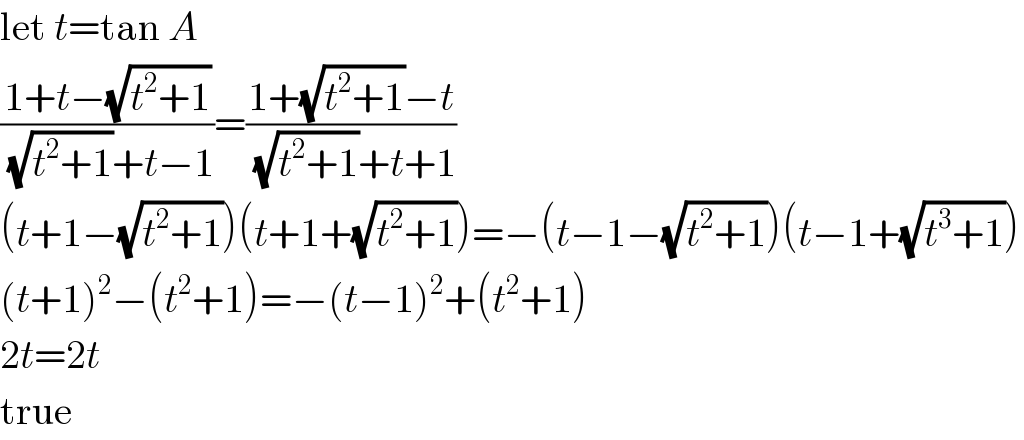
let t=tan A ((1+t−(√(t^2 +1)))/( (√(t^2 +1))+t−1))=((1+(√(t^2 +1))−t)/( (√(t^2 +1))+t+1)) (t+1−(√(t^2 +1)))(t+1+(√(t^2 +1)))=−(t−1−(√(t^2 +1)))(t−1+(√(t^3 +1))) (t+1)^2 −(t^2 +1)=−(t−1)^2 +(t^2 +1) 2t=2t true
$$\mathrm{let}\:{t}=\mathrm{tan}\:{A} \\ $$$$\frac{\mathrm{1}+{t}−\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}}{\:\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}+{t}−\mathrm{1}}=\frac{\mathrm{1}+\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}−{t}}{\:\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}+{t}+\mathrm{1}} \\ $$$$\left({t}+\mathrm{1}−\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}\right)\left({t}+\mathrm{1}+\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}\right)=−\left({t}−\mathrm{1}−\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}\right)\left({t}−\mathrm{1}+\sqrt{{t}^{\mathrm{3}} +\mathrm{1}}\right) \\ $$$$\left({t}+\mathrm{1}\right)^{\mathrm{2}} −\left({t}^{\mathrm{2}} +\mathrm{1}\right)=−\left({t}−\mathrm{1}\right)^{\mathrm{2}} +\left({t}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$$\mathrm{2}{t}=\mathrm{2}{t} \\ $$$$\mathrm{true} \\ $$
Answered by MJS_new last updated on 14/Nov/20
((1+(s/c)−(1/c))/((1/c)+(s/c)−1))=((1+(1/c)−(s/c))/((1/c)+(s/c)+1)) (((c+s−1)/c)/((1+s−c)/c))=(((c+1−s)/c)/((1+s+c)/c)) ((c+s−1)/(−c+s+1))=((c−s+1)/(c+s+1)) (c+s−1)(c+s+1)=(c−s+1)(−c+s+1) c^2 +s^2 +2cs−1=−c^2 −s^2 +2cs+1 2cs=2cs true
$$\frac{\mathrm{1}+\frac{{s}}{{c}}−\frac{\mathrm{1}}{{c}}}{\frac{\mathrm{1}}{{c}}+\frac{{s}}{{c}}−\mathrm{1}}=\frac{\mathrm{1}+\frac{\mathrm{1}}{{c}}−\frac{{s}}{{c}}}{\frac{\mathrm{1}}{{c}}+\frac{{s}}{{c}}+\mathrm{1}} \\ $$$$\frac{\frac{{c}+{s}−\mathrm{1}}{{c}}}{\frac{\mathrm{1}+{s}−{c}}{{c}}}=\frac{\frac{{c}+\mathrm{1}−{s}}{{c}}}{\frac{\mathrm{1}+{s}+{c}}{{c}}} \\ $$$$\frac{{c}+{s}−\mathrm{1}}{−{c}+{s}+\mathrm{1}}=\frac{{c}−{s}+\mathrm{1}}{{c}+{s}+\mathrm{1}} \\ $$$$\left({c}+{s}−\mathrm{1}\right)\left({c}+{s}+\mathrm{1}\right)=\left({c}−{s}+\mathrm{1}\right)\left(−{c}+{s}+\mathrm{1}\right) \\ $$$${c}^{\mathrm{2}} +{s}^{\mathrm{2}} +\mathrm{2}{cs}−\mathrm{1}=−{c}^{\mathrm{2}} −{s}^{\mathrm{2}} +\mathrm{2}{cs}+\mathrm{1} \\ $$$$\mathrm{2}{cs}=\mathrm{2}{cs} \\ $$$$\mathrm{true} \\ $$
Answered by ajfour last updated on 14/Nov/20
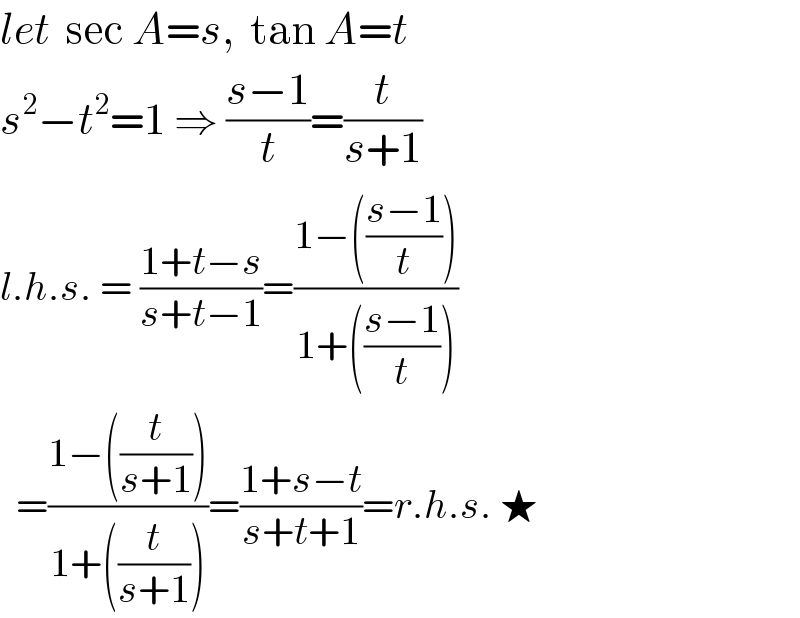
let sec A=s, tan A=t s^2 −t^2 =1 ⇒ ((s−1)/t)=(t/(s+1)) l.h.s. = ((1+t−s)/(s+t−1))=((1−(((s−1)/t)))/(1+(((s−1)/t)))) =((1−((t/(s+1))))/(1+((t/(s+1)))))=((1+s−t)/(s+t+1))=r.h.s. ★
$${let}\:\:\mathrm{sec}\:{A}={s},\:\:\mathrm{tan}\:{A}={t} \\ $$$${s}^{\mathrm{2}} −{t}^{\mathrm{2}} =\mathrm{1}\:\Rightarrow\:\frac{{s}−\mathrm{1}}{{t}}=\frac{{t}}{{s}+\mathrm{1}} \\ $$$${l}.{h}.{s}.\:=\:\frac{\mathrm{1}+{t}−{s}}{{s}+{t}−\mathrm{1}}=\frac{\mathrm{1}−\left(\frac{{s}−\mathrm{1}}{{t}}\right)}{\mathrm{1}+\left(\frac{{s}−\mathrm{1}}{{t}}\right)} \\ $$$$\:\:=\frac{\mathrm{1}−\left(\frac{{t}}{{s}+\mathrm{1}}\right)}{\mathrm{1}+\left(\frac{{t}}{{s}+\mathrm{1}}\right)}=\frac{\mathrm{1}+{s}−{t}}{{s}+{t}+\mathrm{1}}={r}.{h}.{s}.\:\bigstar \\ $$
Commented by peter frank last updated on 14/Nov/20
thank you both
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{both} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *