Menu Close

Question-122098

Tinku Tara 0 Comments
Pin




Question Number 122098 by Rohit412 last updated on 14/Nov/20
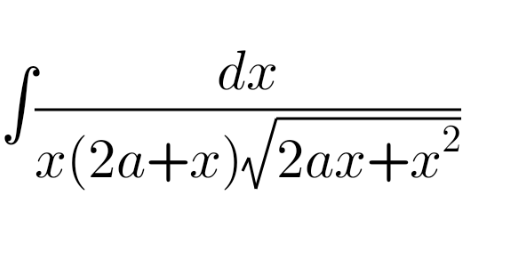
Commented by liberty last updated on 14/Nov/20
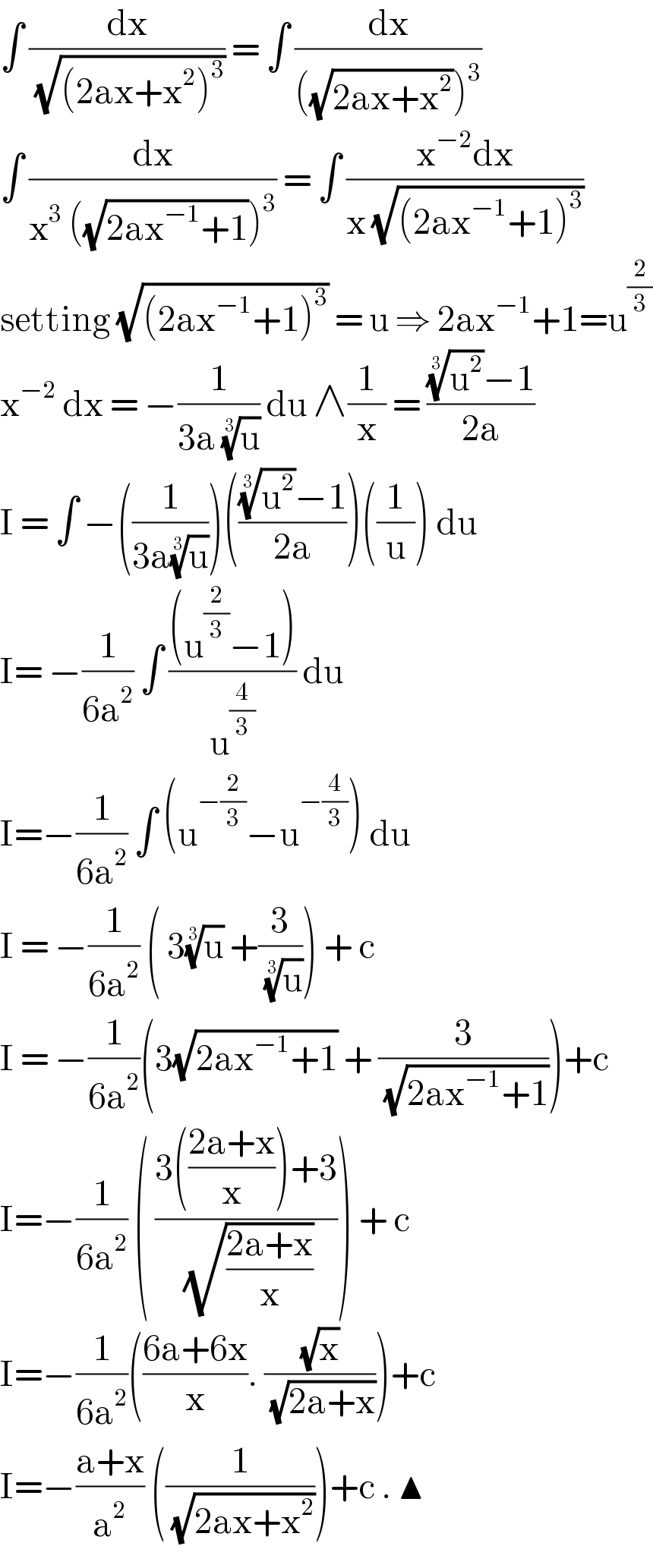
∫ (dx/( (√((2ax+x^2 )^3 )))) = ∫ (dx/(((√(2ax+x^2 )))^3 )) ∫ (dx/(x^3 ((√(2ax^(−1) +1)))^3 )) = ∫ ((x^(−2) dx)/(x (√((2ax^(−1) +1)^3 )))) setting (√((2ax^(−1) +1)^3 )) = u ⇒ 2ax^(−1) +1=u^(2/3) x^(−2) dx = −(1/(3a (u)^(1/3) )) du ∧(1/x) = (((u^2 )^(1/3) −1)/(2a)) I = ∫ −((1/(3a(u)^(1/3) )))((((u^2 )^(1/3) −1)/(2a)))((1/u)) du I= −(1/(6a^2 )) ∫ (((u^(2/3) −1))/u^(4/3) ) du I=−(1/(6a^2 )) ∫ (u^(−(2/3)) −u^(−(4/3)) ) du I = −(1/(6a^2 )) ( 3(u)^(1/3) +(3/( (u)^(1/3) ))) + c I = −(1/(6a^2 ))(3(√(2ax^(−1) +1)) + (3/( (√(2ax^(−1) +1)))))+c I=−(1/(6a^2 )) ( ((3(((2a+x)/x))+3)/( (√((2a+x)/x))))) + c I=−(1/(6a^2 ))(((6a+6x)/x). ((√x)/( (√(2a+x)))))+c I=−((a+x)/a^2 ) ((1/( (√(2ax+x^2 )))))+c . ▲
$$\int\:\frac{\mathrm{dx}}{\:\sqrt{\left(\mathrm{2ax}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{3}} }}\:=\:\int\:\frac{\mathrm{dx}}{\left(\sqrt{\mathrm{2ax}+\mathrm{x}^{\mathrm{2}} }\right)^{\mathrm{3}} } \\ $$$$\int\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{3}} \:\left(\sqrt{\mathrm{2ax}^{−\mathrm{1}} +\mathrm{1}}\right)^{\mathrm{3}} }\:=\:\int\:\frac{\mathrm{x}^{−\mathrm{2}} \mathrm{dx}}{\mathrm{x}\:\sqrt{\left(\mathrm{2ax}^{−\mathrm{1}} +\mathrm{1}\right)^{\mathrm{3}} }} \\ $$$$\mathrm{setting}\:\sqrt{\left(\mathrm{2ax}^{−\mathrm{1}} +\mathrm{1}\right)^{\mathrm{3}} }\:=\:\mathrm{u}\:\Rightarrow\:\mathrm{2ax}^{−\mathrm{1}} +\mathrm{1}=\mathrm{u}^{\frac{\mathrm{2}}{\mathrm{3}}} \\ $$$$\mathrm{x}^{−\mathrm{2}} \:\mathrm{dx}\:=\:−\frac{\mathrm{1}}{\mathrm{3a}\:\sqrt[{\mathrm{3}}]{\mathrm{u}}}\:\mathrm{du}\:\wedge\frac{\mathrm{1}}{\mathrm{x}}\:=\:\frac{\sqrt[{\mathrm{3}}]{\mathrm{u}^{\mathrm{2}} }−\mathrm{1}}{\mathrm{2a}} \\ $$$$\mathrm{I}\:=\:\int\:−\left(\frac{\mathrm{1}}{\mathrm{3a}\sqrt[{\mathrm{3}}]{\mathrm{u}}}\right)\left(\frac{\sqrt[{\mathrm{3}}]{\mathrm{u}^{\mathrm{2}} }−\mathrm{1}}{\mathrm{2a}}\right)\left(\frac{\mathrm{1}}{\mathrm{u}}\right)\:\mathrm{du}\: \\ $$$$\mathrm{I}=\:−\frac{\mathrm{1}}{\mathrm{6a}^{\mathrm{2}} }\:\int\:\frac{\left(\mathrm{u}^{\frac{\mathrm{2}}{\mathrm{3}}} −\mathrm{1}\right)}{\mathrm{u}^{\frac{\mathrm{4}}{\mathrm{3}}} }\:\mathrm{du}\: \\ $$$$\mathrm{I}=−\frac{\mathrm{1}}{\mathrm{6a}^{\mathrm{2}} }\:\int\:\left(\mathrm{u}^{−\frac{\mathrm{2}}{\mathrm{3}}} −\mathrm{u}^{−\frac{\mathrm{4}}{\mathrm{3}}} \right)\:\mathrm{du}\: \\ $$$$\mathrm{I}\:=\:−\frac{\mathrm{1}}{\mathrm{6a}^{\mathrm{2}} }\:\left(\:\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{u}}\:+\frac{\mathrm{3}}{\:\sqrt[{\mathrm{3}}]{\mathrm{u}}}\right)\:+\:\mathrm{c}\: \\ $$$$\mathrm{I}\:=\:−\frac{\mathrm{1}}{\mathrm{6a}^{\mathrm{2}} }\left(\mathrm{3}\sqrt{\mathrm{2ax}^{−\mathrm{1}} +\mathrm{1}}\:+\:\frac{\mathrm{3}}{\:\sqrt{\mathrm{2ax}^{−\mathrm{1}} +\mathrm{1}}}\right)+\mathrm{c} \\ $$$$\mathrm{I}=−\frac{\mathrm{1}}{\mathrm{6a}^{\mathrm{2}} }\:\left(\:\frac{\mathrm{3}\left(\frac{\mathrm{2a}+\mathrm{x}}{\mathrm{x}}\right)+\mathrm{3}}{\:\sqrt{\frac{\mathrm{2a}+\mathrm{x}}{\mathrm{x}}}}\right)\:+\:\mathrm{c}\: \\ $$$$\mathrm{I}=−\frac{\mathrm{1}}{\mathrm{6a}^{\mathrm{2}} }\left(\frac{\mathrm{6a}+\mathrm{6x}}{\mathrm{x}}.\:\frac{\sqrt{\mathrm{x}}}{\:\sqrt{\mathrm{2a}+\mathrm{x}}}\right)+\mathrm{c}\: \\ $$$$\mathrm{I}=−\frac{\mathrm{a}+\mathrm{x}}{\mathrm{a}^{\mathrm{2}} }\:\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2ax}+\mathrm{x}^{\mathrm{2}} }}\right)+\mathrm{c}\:.\:\blacktriangle \\ $$
Answered by ajfour last updated on 14/Nov/20
I=∫(dx/((2ax+x^2 )^(3/2) ))=∫(dx/({(x+a)^2 −a^2 }^(3/2) )) let x+a=asec θ ⇒ dx=asec θtan θdθ I=∫ ((asec θtan θdθ)/(a^3 tan^3 θ)) = (1/a^2 )∫((cos θ)/(sin^2 θ))dθ Now let sin θ=t ⇒ cos θdθ=dt ⇒ I=(1/a^2 )∫(dt/t^2 ) = −(1/(a^2 t))+c =− (1/(a^2 sin θ))+c I =−((1/a^2 )/( (√(1−(a^2 /((x+a)^2 ))))))+c I=((−∣x+a∣)/(a^2 (√(x^2 +2ax))))+c .
$${I}=\int\frac{{dx}}{\left(\mathrm{2}{ax}+{x}^{\mathrm{2}} \right)^{\mathrm{3}/\mathrm{2}} }=\int\frac{{dx}}{\left\{\left({x}+{a}\right)^{\mathrm{2}} −{a}^{\mathrm{2}} \right\}^{\mathrm{3}/\mathrm{2}} } \\ $$$${let}\:{x}+{a}={a}\mathrm{sec}\:\theta \\ $$$$\Rightarrow\:\:{dx}={a}\mathrm{sec}\:\theta\mathrm{tan}\:\theta{d}\theta \\ $$$${I}=\int\:\frac{{a}\mathrm{sec}\:\theta\mathrm{tan}\:\theta{d}\theta}{{a}^{\mathrm{3}} \mathrm{tan}\:^{\mathrm{3}} \theta}\:=\:\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\int\frac{\mathrm{cos}\:\theta}{\mathrm{sin}\:^{\mathrm{2}} \theta}{d}\theta \\ $$$$\:\:{Now}\:\:{let}\:\:\mathrm{sin}\:\theta={t}\:\:\Rightarrow\:\:\mathrm{cos}\:\theta{d}\theta={dt} \\ $$$$\Rightarrow\:{I}=\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\int\frac{{dt}}{{t}^{\mathrm{2}} }\:=\:−\frac{\mathrm{1}}{{a}^{\mathrm{2}} {t}}+{c}\:=−\:\frac{\mathrm{1}}{{a}^{\mathrm{2}} \mathrm{sin}\:\theta}+{c} \\ $$$$\:\:{I}\:=−\frac{\mathrm{1}/{a}^{\mathrm{2}} }{\:\sqrt{\mathrm{1}−\frac{{a}^{\mathrm{2}} }{\left({x}+{a}\right)^{\mathrm{2}} }}}+{c}\:\: \\ $$$$\:{I}=\frac{−\mid{x}+{a}\mid}{{a}^{\mathrm{2}} \sqrt{{x}^{\mathrm{2}} +\mathrm{2}{ax}}}+{c}\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *