Menu Close

Question-122111

Tinku Tara 0 Comments
Pin




Question Number 122111 by ajfour last updated on 14/Nov/20
Commented by ajfour last updated on 14/Nov/20
Find sides of maximum area right angled triangle inscribed in an ellipse.
$${Find}\:{sides}\:{of}\:{maximum}\:{area} \\ $$$${right}\:{angled}\:{triangle}\:{inscribed} \\ $$$${in}\:{an}\:{ellipse}. \\ $$
Commented by MJS_new last updated on 14/Nov/20
it′s part of the problem to find the general triangle with maximum area. I solved it, cannot find the old question. all triangles with centroid in the center of the ellipse have equal area. we have to find the rectangular triangles out of these
$$\mathrm{it}'\mathrm{s}\:\mathrm{part}\:\mathrm{of}\:\mathrm{the}\:\mathrm{problem}\:\mathrm{to}\:\mathrm{find}\:\mathrm{the}\:\mathrm{general} \\ $$$$\mathrm{triangle}\:\mathrm{with}\:\mathrm{maximum}\:\mathrm{area}.\:\mathrm{I}\:\mathrm{solved}\:\mathrm{it}, \\ $$$$\mathrm{cannot}\:\mathrm{find}\:\mathrm{the}\:\mathrm{old}\:\mathrm{question}. \\ $$$$\mathrm{all}\:\mathrm{triangles}\:\mathrm{with}\:\mathrm{centroid}\:\mathrm{in}\:\mathrm{the}\:\mathrm{center}\:\mathrm{of} \\ $$$$\mathrm{the}\:\mathrm{ellipse}\:\mathrm{have}\:\mathrm{equal}\:\mathrm{area}.\:\mathrm{we}\:\mathrm{have}\:\mathrm{to}\:\mathrm{find} \\ $$$$\mathrm{the}\:\mathrm{rectangular}\:\mathrm{triangles}\:\mathrm{out}\:\mathrm{of}\:\mathrm{these} \\ $$
Commented by MJS_new last updated on 14/Nov/20
I only have the formulas for the axes of the smallest ellipse around a given triangle with sides a, b, c which is (1/3)(√(a^2 +b^2 +c^2 ±2(√(a^2 b^2 +a^2 c^2 +b^2 c^2 −δ^2 )))) where δ=(√((a+b+c)(a+b−c)(a+c−b)(b+c−a))) if we let c=(√(a^2 +b^2 )) we get ((√2)/3)(√(a^2 +b^2 ±(√(a^4 −a^2 b^2 +b^4 )))) we have to solve this for a, b with given axes α, β: { ((α=((√2)/3)(√(a^2 +b^2 +(√(a^4 −a^2 b^2 +b^4 )))))),((β=((√2)/3)(√(a^2 +b^2 −(√(a^4 −a^2 b^2 +b^4 )))))) :} sorry I have got no time right now
$$\mathrm{I}\:\mathrm{only}\:\mathrm{have}\:\mathrm{the}\:\mathrm{formulas}\:\mathrm{for}\:\mathrm{the}\:\mathrm{axes}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{smallest}\:\mathrm{ellipse}\:\mathrm{around}\:\mathrm{a}\:\mathrm{given}\:\mathrm{triangle}\:\mathrm{with} \\ $$$$\mathrm{sides}\:{a},\:{b},\:{c}\:\mathrm{which}\:\mathrm{is} \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \pm\mathrm{2}\sqrt{{a}^{\mathrm{2}} {b}^{\mathrm{2}} +{a}^{\mathrm{2}} {c}^{\mathrm{2}} +{b}^{\mathrm{2}} {c}^{\mathrm{2}} −\delta^{\mathrm{2}} }} \\ $$$$\mathrm{where}\:\delta=\sqrt{\left({a}+{b}+{c}\right)\left({a}+{b}−{c}\right)\left({a}+{c}−{b}\right)\left({b}+{c}−{a}\right)} \\ $$$$\mathrm{if}\:\mathrm{we}\:\mathrm{let}\:{c}=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\:\mathrm{we}\:\mathrm{get} \\ $$$$\frac{\sqrt{\mathrm{2}}}{\mathrm{3}}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} \pm\sqrt{{a}^{\mathrm{4}} −{a}^{\mathrm{2}} {b}^{\mathrm{2}} +{b}^{\mathrm{4}} }} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{this}\:\mathrm{for}\:{a},\:{b}\:\mathrm{with}\:\mathrm{given} \\ $$$$\mathrm{axes}\:\alpha,\:\beta: \\ $$$$\begin{cases}{\alpha=\frac{\sqrt{\mathrm{2}}}{\mathrm{3}}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\sqrt{{a}^{\mathrm{4}} −{a}^{\mathrm{2}} {b}^{\mathrm{2}} +{b}^{\mathrm{4}} }}}\\{\beta=\frac{\sqrt{\mathrm{2}}}{\mathrm{3}}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\sqrt{{a}^{\mathrm{4}} −{a}^{\mathrm{2}} {b}^{\mathrm{2}} +{b}^{\mathrm{4}} }}}\end{cases} \\ $$$$\mathrm{sorry}\:\mathrm{I}\:\mathrm{have}\:\mathrm{got}\:\mathrm{no}\:\mathrm{time}\:\mathrm{right}\:\mathrm{now} \\ $$
Commented by MJS_new last updated on 14/Nov/20
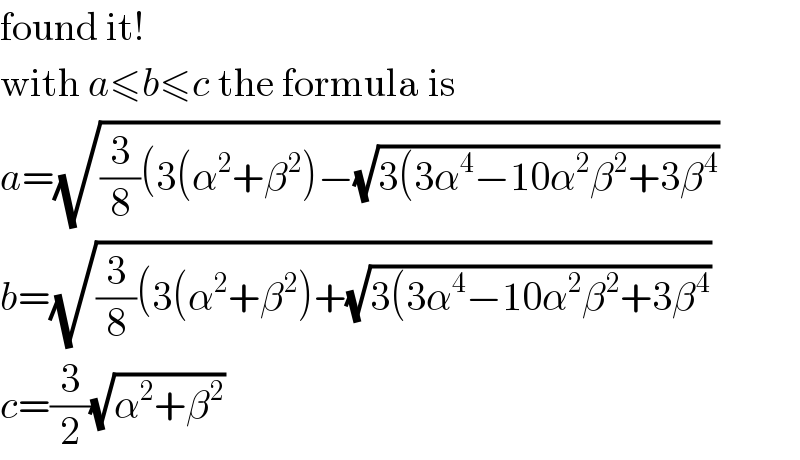
found it! with a≤b≤c the formula is a=(√((3/8)(3(α^2 +β^2 )−(√(3(3α^4 −10α^2 β^2 +3β^4 )))) b=(√((3/8)(3(α^2 +β^2 )+(√(3(3α^4 −10α^2 β^2 +3β^4 )))) c=(3/2)(√(α^2 +β^2 ))
$$\mathrm{found}\:\mathrm{it}! \\ $$$$\mathrm{with}\:{a}\leqslant{b}\leqslant{c}\:\mathrm{the}\:\mathrm{formula}\:\mathrm{is} \\ $$$${a}=\sqrt{\frac{\mathrm{3}}{\mathrm{8}}\left(\mathrm{3}\left(\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} \right)−\sqrt{\mathrm{3}\left(\mathrm{3}\alpha^{\mathrm{4}} −\mathrm{10}\alpha^{\mathrm{2}} \beta^{\mathrm{2}} +\mathrm{3}\beta^{\mathrm{4}} \right.}\right.} \\ $$$${b}=\sqrt{\frac{\mathrm{3}}{\mathrm{8}}\left(\mathrm{3}\left(\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} \right)+\sqrt{\mathrm{3}\left(\mathrm{3}\alpha^{\mathrm{4}} −\mathrm{10}\alpha^{\mathrm{2}} \beta^{\mathrm{2}} +\mathrm{3}\beta^{\mathrm{4}} \right.}\right.} \\ $$$${c}=\frac{\mathrm{3}}{\mathrm{2}}\sqrt{\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} } \\ $$
Commented by ajfour last updated on 14/Nov/20
Thanks a lot Sir, a glimpse of these formulas proves that the proof isn′t an easy one, though..
$${Thanks}\:{a}\:{lot}\:{Sir},\:{a}\:{glimpse}\:{of} \\ $$$${these}\:{formulas}\:{proves}\:\:{that}\:{the} \\ $$$${proof}\:{isn}'{t}\:{an}\:{easy}\:{one},\:{though}.. \\ $$
Commented by MJS_new last updated on 14/Nov/20
my idea had been to start with a unit circle and an inscribed equilateral triangle then first rotate the triangle by ϕ and second compress the whole thing to get the desired ellipse. this way it′s obvious that the centroid stays in the center and all triangles you get have the same area and there′s no triangle with a greater area. I wanted to find the smallest ellipse around a given triangle. I kept the formulas but not the path. will send them again but not now
$$\mathrm{my}\:\mathrm{idea}\:\mathrm{had}\:\mathrm{been}\:\mathrm{to}\:\mathrm{start}\:\mathrm{with}\:\mathrm{a}\:\mathrm{unit}\:\mathrm{circle} \\ $$$$\mathrm{and}\:\mathrm{an}\:\mathrm{inscribed}\:\mathrm{equilateral}\:\mathrm{triangle} \\ $$$$\mathrm{then}\:\mathrm{first}\:\mathrm{rotate}\:\mathrm{the}\:\mathrm{triangle}\:\mathrm{by}\:\varphi\:\mathrm{and}\:\mathrm{second} \\ $$$$\mathrm{compress}\:\mathrm{the}\:\mathrm{whole}\:\mathrm{thing}\:\mathrm{to}\:\mathrm{get}\:\mathrm{the}\:\mathrm{desired} \\ $$$$\mathrm{ellipse}.\:\mathrm{this}\:\mathrm{way}\:\mathrm{it}'\mathrm{s}\:\mathrm{obvious}\:\mathrm{that}\:\mathrm{the}\:\mathrm{centroid} \\ $$$$\mathrm{stays}\:\mathrm{in}\:\mathrm{the}\:\mathrm{center}\:\mathrm{and}\:\mathrm{all}\:\mathrm{triangles}\:\mathrm{you}\:\mathrm{get} \\ $$$$\mathrm{have}\:\mathrm{the}\:\mathrm{same}\:\mathrm{area}\:\mathrm{and}\:\mathrm{there}'\mathrm{s}\:\mathrm{no}\:\mathrm{triangle} \\ $$$$\mathrm{with}\:\mathrm{a}\:\mathrm{greater}\:\mathrm{area}. \\ $$$$\mathrm{I}\:\mathrm{wanted}\:\mathrm{to}\:\mathrm{find}\:\mathrm{the}\:\mathrm{smallest}\:\mathrm{ellipse}\:\mathrm{around} \\ $$$$\mathrm{a}\:\mathrm{given}\:\mathrm{triangle}.\:\mathrm{I}\:\mathrm{kept}\:\mathrm{the}\:\mathrm{formulas}\:\mathrm{but}\:\mathrm{not} \\ $$$$\mathrm{the}\:\mathrm{path}.\:\mathrm{will}\:\mathrm{send}\:\mathrm{them}\:\mathrm{again}\:\mathrm{but}\:\mathrm{not}\:\mathrm{now} \\ $$
Commented by MJS_new last updated on 14/Nov/20
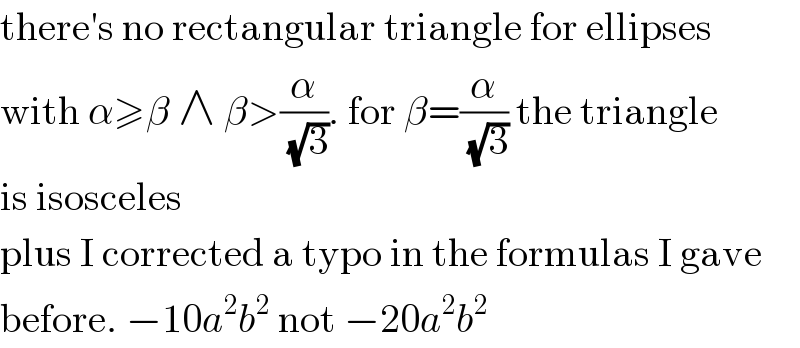
there′s no rectangular triangle for ellipses with α≥β ∧ β>(α/( (√3))). for β=(α/( (√3))) the triangle is isosceles plus I corrected a typo in the formulas I gave before. −10a^2 b^2 not −20a^2 b^2
$$\mathrm{there}'\mathrm{s}\:\mathrm{no}\:\mathrm{rectangular}\:\mathrm{triangle}\:\mathrm{for}\:\mathrm{ellipses} \\ $$$$\mathrm{with}\:\alpha\geqslant\beta\:\wedge\:\beta>\frac{\alpha}{\:\sqrt{\mathrm{3}}}.\:\mathrm{for}\:\beta=\frac{\alpha}{\:\sqrt{\mathrm{3}}}\:\mathrm{the}\:\mathrm{triangle} \\ $$$$\mathrm{is}\:\mathrm{isosceles} \\ $$$$\mathrm{plus}\:\mathrm{I}\:\mathrm{corrected}\:\mathrm{a}\:\mathrm{typo}\:\mathrm{in}\:\mathrm{the}\:\mathrm{formulas}\:\mathrm{I}\:\mathrm{gave} \\ $$$$\mathrm{before}.\:−\mathrm{10}{a}^{\mathrm{2}} {b}^{\mathrm{2}} \:\mathrm{not}\:−\mathrm{20}{a}^{\mathrm{2}} {b}^{\mathrm{2}} \\ $$
Answered by ajfour last updated on 14/Nov/20
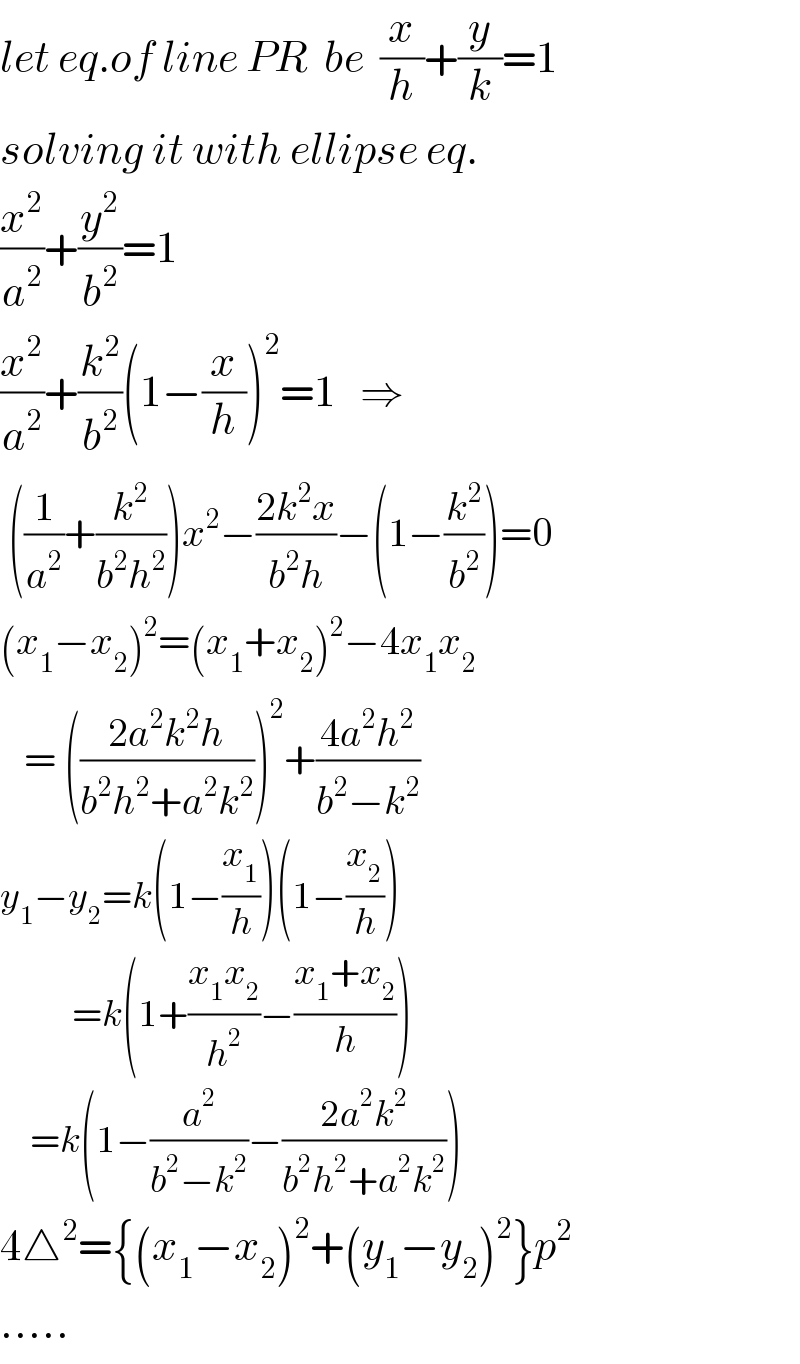
let eq.of line PR be (x/h)+(y/k)=1 solving it with ellipse eq. (x^2 /a^2 )+(y^2 /b^2 )=1 (x^2 /a^2 )+(k^2 /b^2 )(1−(x/h))^2 =1 ⇒ ((1/a^2 )+(k^2 /(b^2 h^2 )))x^2 −((2k^2 x)/(b^2 h))−(1−(k^2 /b^2 ))=0 (x_1 −x_2 )^2 =(x_1 +x_2 )^2 −4x_1 x_2 = (((2a^2 k^2 h)/(b^2 h^2 +a^2 k^2 )))^2 +((4a^2 h^2 )/(b^2 −k^2 )) y_1 −y_2 =k(1−(x_1 /h))(1−(x_2 /h)) =k(1+((x_1 x_2 )/h^2 )−((x_1 +x_2 )/h)) =k(1−(a^2 /(b^2 −k^2 ))−((2a^2 k^2 )/(b^2 h^2 +a^2 k^2 ))) 4△^2 ={(x_1 −x_2 )^2 +(y_1 −y_2 )^2 }p^2 .....
$${let}\:{eq}.{of}\:{line}\:{PR}\:\:{be}\:\:\frac{{x}}{{h}}+\frac{{y}}{{k}}=\mathrm{1} \\ $$$${solving}\:{it}\:{with}\:{ellipse}\:{eq}. \\ $$$$\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{k}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\left(\mathrm{1}−\frac{{x}}{{h}}\right)^{\mathrm{2}} =\mathrm{1}\:\:\:\Rightarrow \\ $$$$\:\left(\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{{k}^{\mathrm{2}} }{{b}^{\mathrm{2}} {h}^{\mathrm{2}} }\right){x}^{\mathrm{2}} −\frac{\mathrm{2}{k}^{\mathrm{2}} {x}}{{b}^{\mathrm{2}} {h}}−\left(\mathrm{1}−\frac{{k}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\right)=\mathrm{0} \\ $$$$\left({x}_{\mathrm{1}} −{x}_{\mathrm{2}} \right)^{\mathrm{2}} =\left({x}_{\mathrm{1}} +{x}_{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{4}{x}_{\mathrm{1}} {x}_{\mathrm{2}} \\ $$$$\:\:\:=\:\left(\frac{\mathrm{2}{a}^{\mathrm{2}} {k}^{\mathrm{2}} {h}}{{b}^{\mathrm{2}} {h}^{\mathrm{2}} +{a}^{\mathrm{2}} {k}^{\mathrm{2}} }\right)^{\mathrm{2}} +\frac{\mathrm{4}{a}^{\mathrm{2}} {h}^{\mathrm{2}} }{{b}^{\mathrm{2}} −{k}^{\mathrm{2}} } \\ $$$${y}_{\mathrm{1}} −{y}_{\mathrm{2}} ={k}\left(\mathrm{1}−\frac{{x}_{\mathrm{1}} }{{h}}\right)\left(\mathrm{1}−\frac{{x}_{\mathrm{2}} }{{h}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:={k}\left(\mathrm{1}+\frac{{x}_{\mathrm{1}} {x}_{\mathrm{2}} }{{h}^{\mathrm{2}} }−\frac{{x}_{\mathrm{1}} +{x}_{\mathrm{2}} }{{h}}\right) \\ $$$$\:\:\:\:\:={k}\left(\mathrm{1}−\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} −{k}^{\mathrm{2}} }−\frac{\mathrm{2}{a}^{\mathrm{2}} {k}^{\mathrm{2}} }{{b}^{\mathrm{2}} {h}^{\mathrm{2}} +{a}^{\mathrm{2}} {k}^{\mathrm{2}} }\right) \\ $$$$\mathrm{4}\bigtriangleup^{\mathrm{2}} =\left\{\left({x}_{\mathrm{1}} −{x}_{\mathrm{2}} \right)^{\mathrm{2}} +\left({y}_{\mathrm{1}} −{y}_{\mathrm{2}} \right)^{\mathrm{2}} \right\}{p}^{\mathrm{2}} \\ $$$$….. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *