Question Number 122137 by sdfg last updated on 14/Nov/20
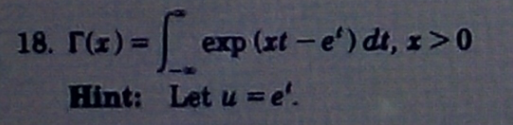
Answered by Bird last updated on 14/Nov/20
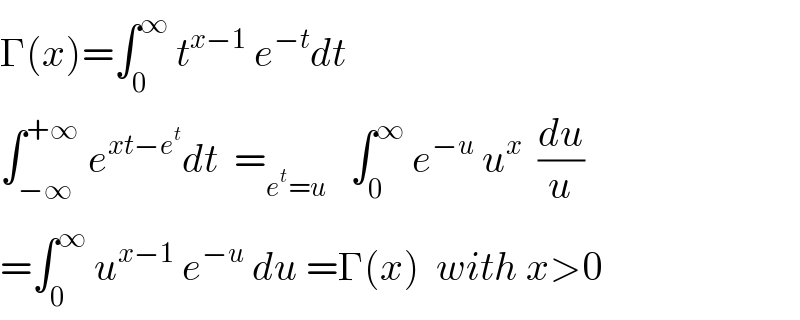
$$\Gamma\left({x}\right)=\int_{\mathrm{0}} ^{\infty} \:{t}^{{x}−\mathrm{1}} \:{e}^{−{t}} {dt} \\ $$$$\int_{−\infty} ^{+\infty} \:{e}^{{xt}−{e}^{{t}} } {dt}\:\:=_{{e}^{{t}} ={u}} \:\:\:\int_{\mathrm{0}} ^{\infty} \:{e}^{−{u}} \:{u}^{{x}} \:\:\frac{{du}}{{u}} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:{u}^{{x}−\mathrm{1}} \:{e}^{−{u}} \:{du}\:=\Gamma\left({x}\right)\:\:{with}\:{x}>\mathrm{0} \\ $$
