Question Number 122214 by peter frank last updated on 14/Nov/20
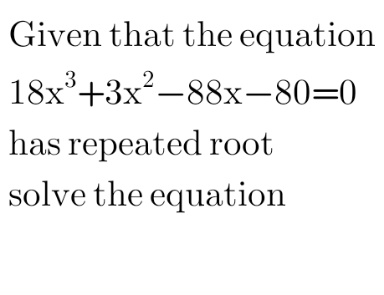
Answered by floor(10²Eta[1]) last updated on 14/Nov/20

$$\mathrm{if}\:\mathrm{f}\left(\mathrm{x}\right)\:\mathrm{has}\:\mathrm{a}\:\mathrm{repeated}\:\mathrm{root}\:\mathrm{so}\:\mathrm{f}'\left(\mathrm{x}\right)\:\mathrm{has}\:\mathrm{that}\:\mathrm{root} \\ $$$$\mathrm{f}'\left(\mathrm{x}\right)=\mathrm{54x}^{\mathrm{2}} +\mathrm{6x}−\mathrm{88}=\mathrm{0}=\mathrm{27x}^{\mathrm{2}} +\mathrm{3x}−\mathrm{44} \\ $$$$\mathrm{x}=\frac{−\mathrm{1}\pm\sqrt{\mathrm{1}+\mathrm{4}.\mathrm{44}.\mathrm{3}}}{\mathrm{18}}=\frac{−\mathrm{1}\pm\mathrm{23}}{\mathrm{18}} \\ $$$$\mathrm{x}=\frac{\mathrm{11}}{\mathrm{9}}\:\mathrm{or}\:\mathrm{x}=−\frac{\mathrm{4}}{\mathrm{3}} \\ $$$$\mathrm{checking}\:\mathrm{the}\:\mathrm{solutions}\:\mathrm{on}\:\mathrm{the}\:\mathrm{original} \\ $$$$\mathrm{equation}\:\mathrm{you}\:\mathrm{find}\:\mathrm{that}\:\frac{−\mathrm{4}}{\mathrm{3}}\:\mathrm{is}\:\mathrm{a}\:\mathrm{root} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\left(\mathrm{x}+\frac{\mathrm{4}}{\mathrm{3}}\right)^{\mathrm{2}} \left(\mathrm{ax}+\mathrm{b}\right)=\mathrm{18x}^{\mathrm{3}} +\mathrm{3x}^{\mathrm{2}} −\mathrm{88x}−\mathrm{80} \\ $$$$\Rightarrow\left(\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{8x}}{\mathrm{3}}+\frac{\mathrm{16}}{\mathrm{9}}\right)\left(\mathrm{18x}+\mathrm{b}\right)=\mathrm{18x}^{\mathrm{3}} +\left(\mathrm{48}+\mathrm{b}\right)\mathrm{x}^{\mathrm{2}} +\left(\mathrm{32}+\frac{\mathrm{8b}}{\mathrm{3}}\right)\mathrm{x}+\frac{\mathrm{16b}}{\mathrm{9}} \\ $$$$\mathrm{48}+\mathrm{b}=\mathrm{3}\Rightarrow\mathrm{b}=−\mathrm{45} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\left(\mathrm{x}+\frac{\mathrm{4}}{\mathrm{3}}\right)^{\mathrm{2}} \left(\mathrm{18x}−\mathrm{45}\right) \\ $$$$\mathrm{18x}−\mathrm{45}=\mathrm{0}\Rightarrow\mathrm{x}=\frac{\mathrm{5}}{\mathrm{2}} \\ $$$$\mathrm{the}\:\mathrm{roots}\:\mathrm{are}\:\mathrm{x}=\frac{−\mathrm{4}}{\mathrm{3}},\:\frac{−\mathrm{4}}{\mathrm{3}}\:\mathrm{and}\:\frac{\mathrm{5}}{\mathrm{2}} \\ $$
