Question Number 122319 by help last updated on 15/Nov/20
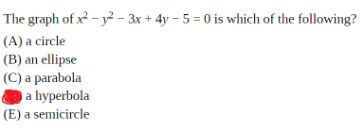
Commented by help last updated on 15/Nov/20
$${explain}\:{your}\:{answer}\:{pls} \\ $$
Answered by 676597498 last updated on 15/Nov/20
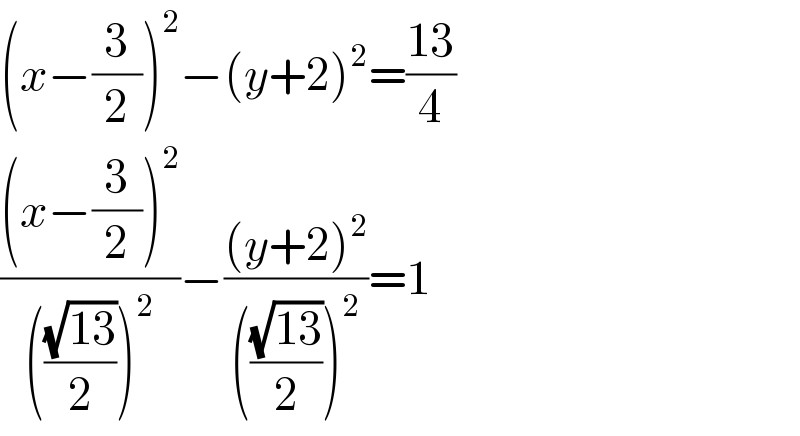
$$\left({x}−\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} −\left({y}+\mathrm{2}\right)^{\mathrm{2}} =\frac{\mathrm{13}}{\mathrm{4}} \\ $$$$\frac{\left({x}−\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} }{\left(\frac{\sqrt{\mathrm{13}}}{\mathrm{2}}\right)^{\mathrm{2}} }−\frac{\left({y}+\mathrm{2}\right)^{\mathrm{2}} }{\left(\frac{\sqrt{\mathrm{13}}}{\mathrm{2}}\right)^{\mathrm{2}} }=\mathrm{1} \\ $$
Answered by MJS_new last updated on 15/Nov/20
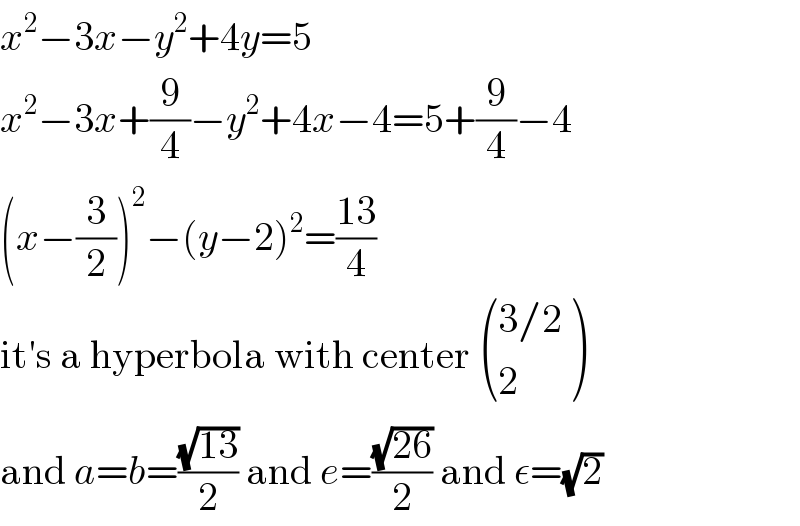
$${x}^{\mathrm{2}} −\mathrm{3}{x}−{y}^{\mathrm{2}} +\mathrm{4}{y}=\mathrm{5} \\ $$$${x}^{\mathrm{2}} −\mathrm{3}{x}+\frac{\mathrm{9}}{\mathrm{4}}−{y}^{\mathrm{2}} +\mathrm{4}{x}−\mathrm{4}=\mathrm{5}+\frac{\mathrm{9}}{\mathrm{4}}−\mathrm{4} \\ $$$$\left({x}−\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} −\left({y}−\mathrm{2}\right)^{\mathrm{2}} =\frac{\mathrm{13}}{\mathrm{4}} \\ $$$$\mathrm{it}'\mathrm{s}\:\mathrm{a}\:\mathrm{hyperbola}\:\mathrm{with}\:\mathrm{center}\:\begin{pmatrix}{\mathrm{3}/\mathrm{2}}\\{\mathrm{2}}\end{pmatrix} \\ $$$$\mathrm{and}\:{a}={b}=\frac{\sqrt{\mathrm{13}}}{\mathrm{2}}\:\mathrm{and}\:{e}=\frac{\sqrt{\mathrm{26}}}{\mathrm{2}}\:\mathrm{and}\:\epsilon=\sqrt{\mathrm{2}} \\ $$
