Question Number 122350 by shaker last updated on 16/Nov/20
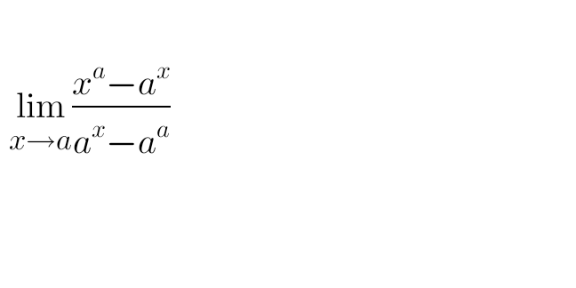
Answered by liberty last updated on 16/Nov/20
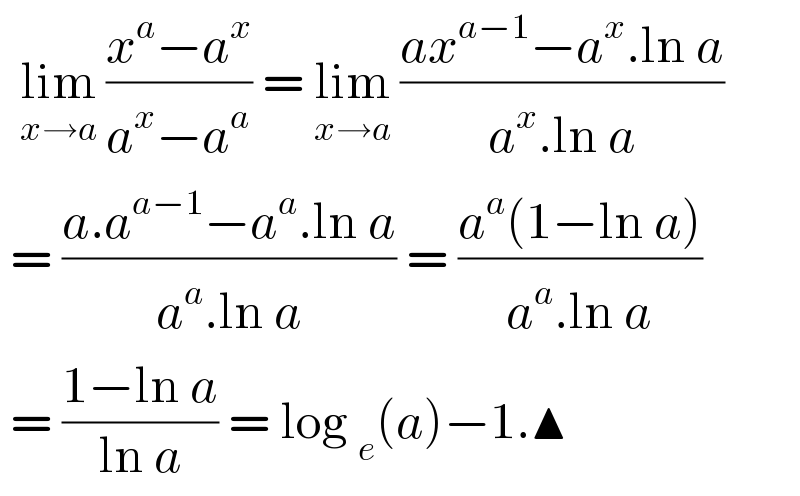
$$\:\:\underset{{x}\rightarrow{a}} {\mathrm{lim}}\:\frac{{x}^{{a}} −{a}^{{x}} }{{a}^{{x}} −{a}^{{a}} }\:=\:\underset{{x}\rightarrow{a}} {\mathrm{lim}}\:\frac{{ax}^{{a}−\mathrm{1}} −{a}^{{x}} .\mathrm{ln}\:{a}}{{a}^{{x}} .\mathrm{ln}\:{a}} \\ $$$$\:=\:\frac{{a}.{a}^{{a}−\mathrm{1}} −{a}^{{a}} .\mathrm{ln}\:{a}}{{a}^{{a}} .\mathrm{ln}\:{a}}\:=\:\frac{{a}^{{a}} \left(\mathrm{1}−\mathrm{ln}\:{a}\right)}{{a}^{{a}} .\mathrm{ln}\:{a}} \\ $$$$\:=\:\frac{\mathrm{1}−\mathrm{ln}\:{a}}{\mathrm{ln}\:{a}}\:=\:\mathrm{log}\:_{{e}} \left({a}\right)−\mathrm{1}.\blacktriangle \\ $$
