Menu Close

Question-122360

Tinku Tara 0 Comments
Pin




Question Number 122360 by benjo_mathlover last updated on 16/Nov/20
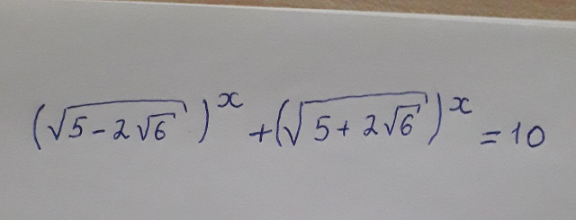
Answered by $@y@m last updated on 16/Nov/20
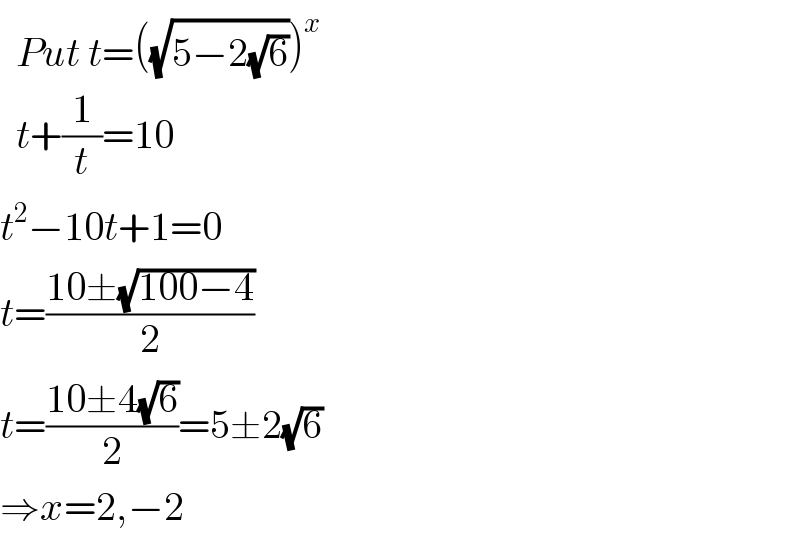
Put t=((√(5−2(√6))))^x t+(1/t)=10 t^2 −10t+1=0 t=((10±(√(100−4)))/2) t=((10±4(√6))/2)=5±2(√6) ⇒x=2,−2
$$\:\:{Put}\:{t}=\left(\sqrt{\mathrm{5}−\mathrm{2}\sqrt{\mathrm{6}}}\right)^{{x}} \\ $$$$\:\:{t}+\frac{\mathrm{1}}{{t}}=\mathrm{10} \\ $$$${t}^{\mathrm{2}} −\mathrm{10}{t}+\mathrm{1}=\mathrm{0} \\ $$$${t}=\frac{\mathrm{10}\pm\sqrt{\mathrm{100}−\mathrm{4}}}{\mathrm{2}} \\ $$$${t}=\frac{\mathrm{10}\pm\mathrm{4}\sqrt{\mathrm{6}}}{\mathrm{2}}=\mathrm{5}\pm\mathrm{2}\sqrt{\mathrm{6}} \\ $$$$\Rightarrow{x}=\mathrm{2},−\mathrm{2} \\ $$
Answered by nimnim last updated on 16/Nov/20
by inspection x=2
$${by}\:{inspection}\:{x}=\mathrm{2} \\ $$
Answered by liberty last updated on 16/Nov/20
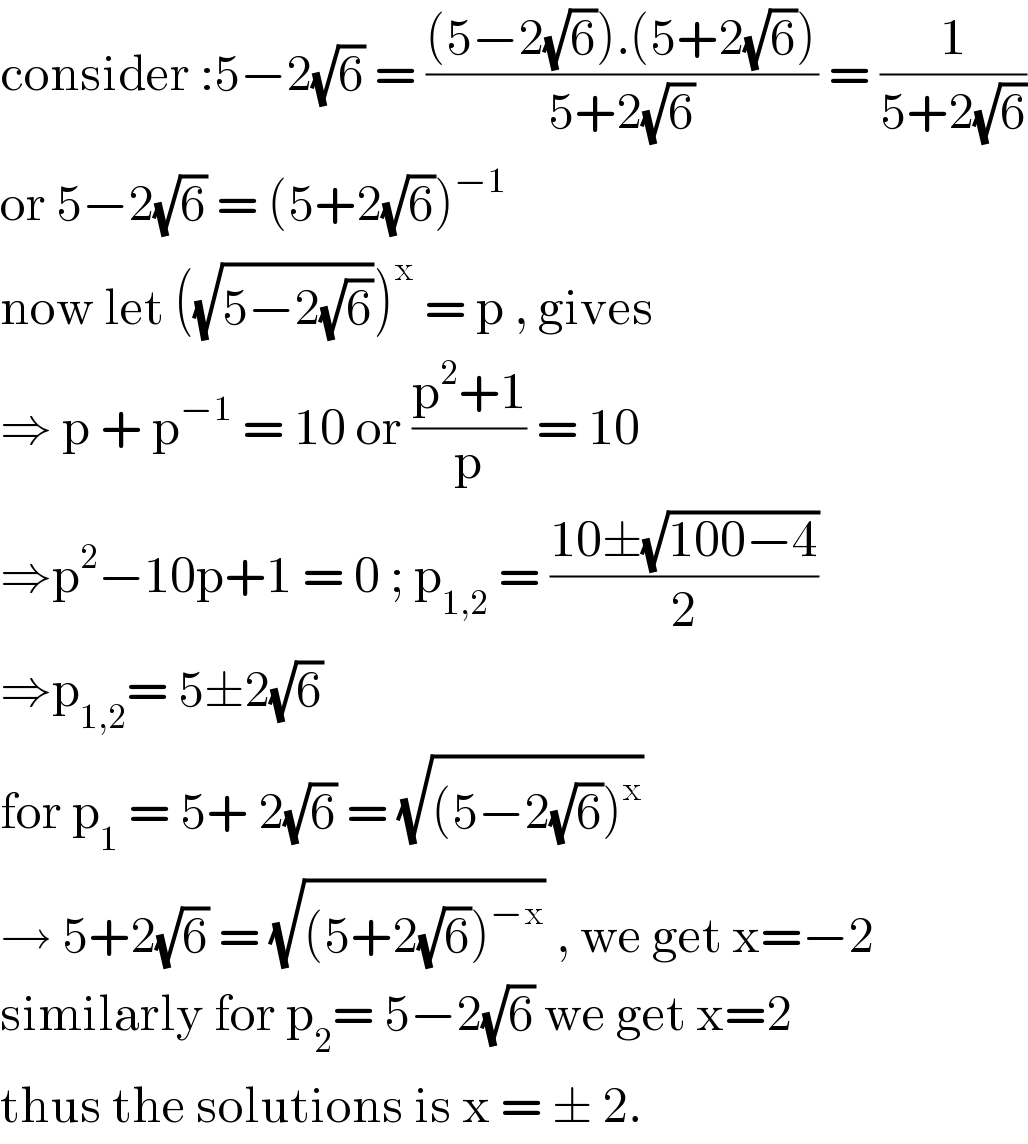
consider :5−2(√6) = (((5−2(√6)).(5+2(√6)))/(5+2(√6))) = (1/(5+2(√6))) or 5−2(√6) = (5+2(√6))^(−1) now let ((√(5−2(√6))))^x = p , gives ⇒ p + p^(−1) = 10 or ((p^2 +1)/p) = 10 ⇒p^2 −10p+1 = 0 ; p_(1,2) = ((10±(√(100−4)))/2) ⇒p_(1,2) = 5±2(√6) for p_1 = 5+ 2(√6) = (√((5−2(√6))^x )) → 5+2(√6) = (√((5+2(√6))^(−x) )) , we get x=−2 similarly for p_2 = 5−2(√6) we get x=2 thus the solutions is x = ± 2.
$$\mathrm{consider}\::\mathrm{5}−\mathrm{2}\sqrt{\mathrm{6}}\:=\:\frac{\left(\mathrm{5}−\mathrm{2}\sqrt{\mathrm{6}}\right).\left(\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}\right)}{\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}}\:=\:\frac{\mathrm{1}}{\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}} \\ $$$$\mathrm{or}\:\mathrm{5}−\mathrm{2}\sqrt{\mathrm{6}}\:=\:\left(\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}\right)^{−\mathrm{1}} \\ $$$$\mathrm{now}\:\mathrm{let}\:\left(\sqrt{\mathrm{5}−\mathrm{2}\sqrt{\mathrm{6}}}\right)^{\mathrm{x}} \:=\:\mathrm{p}\:,\:\mathrm{gives} \\ $$$$\Rightarrow\:\mathrm{p}\:+\:\mathrm{p}^{−\mathrm{1}} \:=\:\mathrm{10}\:\mathrm{or}\:\frac{\mathrm{p}^{\mathrm{2}} +\mathrm{1}}{\mathrm{p}}\:=\:\mathrm{10} \\ $$$$\Rightarrow\mathrm{p}^{\mathrm{2}} −\mathrm{10p}+\mathrm{1}\:=\:\mathrm{0}\:;\:\mathrm{p}_{\mathrm{1},\mathrm{2}} \:=\:\frac{\mathrm{10}\pm\sqrt{\mathrm{100}−\mathrm{4}}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{p}_{\mathrm{1},\mathrm{2}} =\:\mathrm{5}\pm\mathrm{2}\sqrt{\mathrm{6}} \\ $$$$\mathrm{for}\:\mathrm{p}_{\mathrm{1}} \:=\:\mathrm{5}+\:\mathrm{2}\sqrt{\mathrm{6}}\:=\:\sqrt{\left(\mathrm{5}−\mathrm{2}\sqrt{\mathrm{6}}\right)^{\mathrm{x}} } \\ $$$$\rightarrow\:\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}\:=\:\sqrt{\left(\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}\right)^{−\mathrm{x}} }\:,\:\mathrm{we}\:\mathrm{get}\:\mathrm{x}=−\mathrm{2} \\ $$$$\mathrm{similarly}\:\mathrm{for}\:\mathrm{p}_{\mathrm{2}} =\:\mathrm{5}−\mathrm{2}\sqrt{\mathrm{6}}\:\mathrm{we}\:\mathrm{get}\:\mathrm{x}=\mathrm{2} \\ $$$$\mathrm{thus}\:\mathrm{the}\:\mathrm{solutions}\:\mathrm{is}\:\mathrm{x}\:=\:\pm\:\mathrm{2}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *