Menu Close

Question-122377

Tinku Tara 0 Comments
Pin




Question Number 122377 by aristarque last updated on 16/Nov/20
Commented by Dwaipayan Shikari last updated on 16/Nov/20
((54(√3)+41(√5)))^(1/3) =(((2(√3)+(√5))^3 ))^(1/3) ((54(√3)−41(√5)))^(1/3) =(√((2(√3)−(√5))^3 )) A=((2(√3)+(√5)+2(√3)−(√5))/( (√3)))=4
$$\sqrt[{\mathrm{3}}]{\mathrm{54}\sqrt{\mathrm{3}}+\mathrm{41}\sqrt{\mathrm{5}}}\:=\sqrt[{\mathrm{3}}]{\left(\mathrm{2}\sqrt{\mathrm{3}}+\sqrt{\mathrm{5}}\right)^{\mathrm{3}} } \\ $$$$\sqrt[{\mathrm{3}}]{\mathrm{54}\sqrt{\mathrm{3}}−\mathrm{41}\sqrt{\mathrm{5}}}=\sqrt{\left(\mathrm{2}\sqrt{\mathrm{3}}−\sqrt{\mathrm{5}}\right)^{\mathrm{3}} } \\ $$$${A}=\frac{\mathrm{2}\sqrt{\mathrm{3}}+\sqrt{\mathrm{5}}+\mathrm{2}\sqrt{\mathrm{3}}−\sqrt{\mathrm{5}}}{\:\sqrt{\mathrm{3}}}=\mathrm{4} \\ $$
Commented by Dwaipayan Shikari last updated on 16/Nov/20
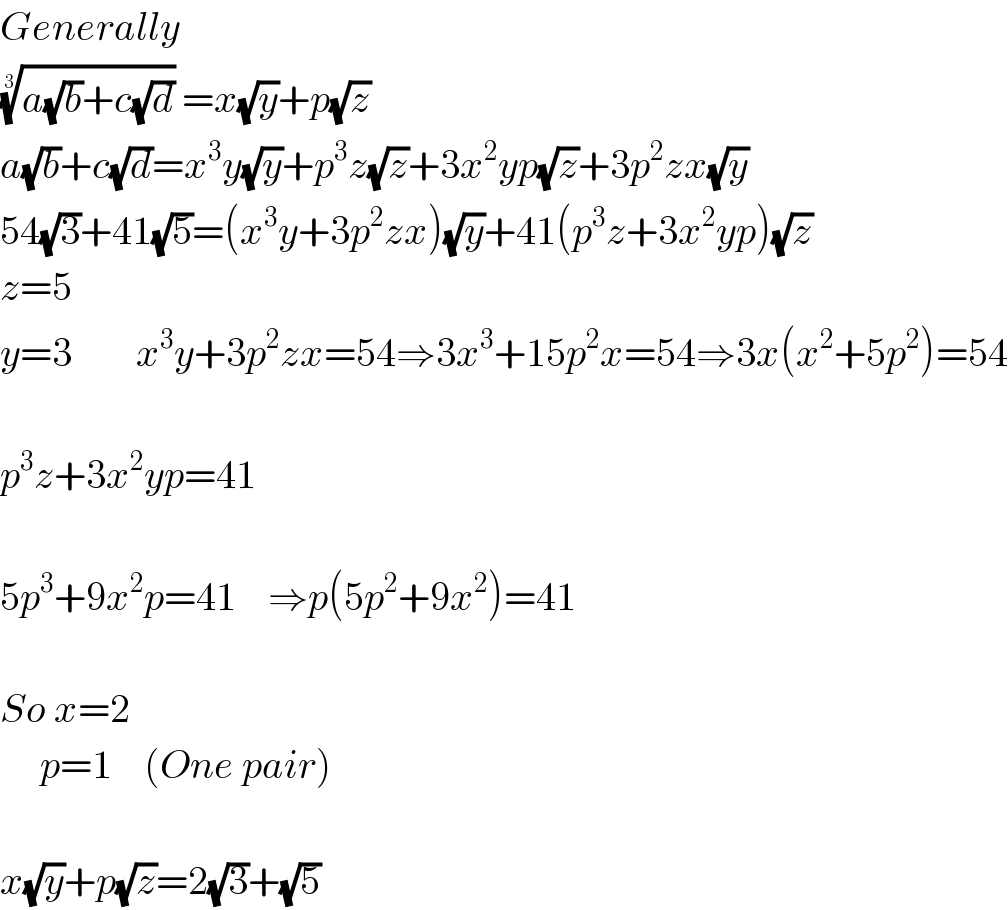
Generally ((a(√b)+c(√d)))^(1/3) =x(√y)+p(√z) a(√b)+c(√d)=x^3 y(√y)+p^3 z(√z)+3x^2 yp(√z)+3p^2 zx(√y) 54(√3)+41(√5)=(x^3 y+3p^2 zx)(√y)+41(p^3 z+3x^2 yp)(√z) z=5 y=3 x^3 y+3p^2 zx=54⇒3x^3 +15p^2 x=54⇒3x(x^2 +5p^2 )=54 p^3 z+3x^2 yp=41 5p^3 +9x^2 p=41 ⇒p(5p^2 +9x^2 )=41 So x=2 p=1 (One pair) x(√y)+p(√z)=2(√3)+(√5)
$${Generally} \\ $$$$\sqrt[{\mathrm{3}}]{{a}\sqrt{{b}}+{c}\sqrt{{d}}}\:={x}\sqrt{{y}}+{p}\sqrt{{z}} \\ $$$${a}\sqrt{{b}}+{c}\sqrt{{d}}={x}^{\mathrm{3}} {y}\sqrt{{y}}+{p}^{\mathrm{3}} {z}\sqrt{{z}}+\mathrm{3}{x}^{\mathrm{2}} {yp}\sqrt{{z}}+\mathrm{3}{p}^{\mathrm{2}} {zx}\sqrt{{y}} \\ $$$$\mathrm{54}\sqrt{\mathrm{3}}+\mathrm{41}\sqrt{\mathrm{5}}=\left({x}^{\mathrm{3}} {y}+\mathrm{3}{p}^{\mathrm{2}} {zx}\right)\sqrt{{y}}+\mathrm{41}\left({p}^{\mathrm{3}} {z}+\mathrm{3}{x}^{\mathrm{2}} {yp}\right)\sqrt{{z}} \\ $$$${z}=\mathrm{5} \\ $$$${y}=\mathrm{3}\:\:\:\:\:\:\:\:{x}^{\mathrm{3}} {y}+\mathrm{3}{p}^{\mathrm{2}} {zx}=\mathrm{54}\Rightarrow\mathrm{3}{x}^{\mathrm{3}} +\mathrm{15}{p}^{\mathrm{2}} {x}=\mathrm{54}\Rightarrow\mathrm{3}{x}\left({x}^{\mathrm{2}} +\mathrm{5}{p}^{\mathrm{2}} \right)=\mathrm{54} \\ $$$$ \\ $$$${p}^{\mathrm{3}} {z}+\mathrm{3}{x}^{\mathrm{2}} {yp}=\mathrm{41} \\ $$$$ \\ $$$$\mathrm{5}{p}^{\mathrm{3}} +\mathrm{9}{x}^{\mathrm{2}} {p}=\mathrm{41}\:\:\:\:\Rightarrow{p}\left(\mathrm{5}{p}^{\mathrm{2}} +\mathrm{9}{x}^{\mathrm{2}} \right)=\mathrm{41} \\ $$$$ \\ $$$${So}\:{x}=\mathrm{2} \\ $$$$\:\:\:\:\:{p}=\mathrm{1}\:\:\:\:\left({One}\:{pair}\right) \\ $$$$ \\ $$$${x}\sqrt{{y}}+{p}\sqrt{{z}}=\mathrm{2}\sqrt{\mathrm{3}}+\sqrt{\mathrm{5}} \\ $$
Commented by Dwaipayan Shikari last updated on 16/Nov/20
On which part?
$${On}\:{which}\:{part}? \\ $$
Commented by aristarque last updated on 16/Nov/20
please i don^. t understand this solution please in detail
$${please}\:{i}\:{do}\boldsymbol{{n}}^{.} \boldsymbol{{t}}\:\boldsymbol{{understand}}\:\boldsymbol{{this}}\:\boldsymbol{{solution}}\:\boldsymbol{{please}}\:\boldsymbol{{in}}\:\boldsymbol{{detail}} \\ $$
Answered by sewak last updated on 17/Nov/20
A=(((54(√3)+41(√5)))^(1/3) /( (√3)))+(((54(√3)−41(√5)))^(1/3) /( (√3))) or, A=((((54(√3)+41(√5)))^(1/3) +((54(√3)−41(√5)))^(1/3) )/( (√3))) or, A=(((54(√3)+41(√5)+54(√3)−41(√5)))^(1/3) /( (√3))) or, A=(((54(√3)+54(√3)))^(1/3) /( (√3))) or, A=(((2×54(√3)))^(1/3) /( (√3))) or, A=(((108(√3)))^(1/3) /( (√3))) or, A=(((3×3×3×4(√3)))^(1/3) /( (√3))) or, A=((3((4(√3)))^(1/3) )/( (√3)))×((√3)/( (√3))) or, A=((3((4(√3)))^(1/3) ×(√3))/( 3)) or, A=((2^2 (√3)))^(1/3) ×(√3) or, A=((√6))^(1/3) ×(√3) or, A=(6)^(1/6) ×(√3) or, A=1.34×1.73=2.3
$$\mathrm{A}=\frac{\sqrt[{\mathrm{3}}]{\mathrm{54}\sqrt{\mathrm{3}}+\mathrm{41}\sqrt{\mathrm{5}}}}{\:\sqrt{\mathrm{3}}}+\frac{\sqrt[{\mathrm{3}}]{\mathrm{54}\sqrt{\mathrm{3}}−\mathrm{41}\sqrt{\mathrm{5}}}}{\:\sqrt{\mathrm{3}}} \\ $$$$\mathrm{or},\:\mathrm{A}=\frac{\sqrt[{\mathrm{3}}]{\mathrm{54}\sqrt{\mathrm{3}}+\mathrm{41}\sqrt{\mathrm{5}}}+\sqrt[{\mathrm{3}}]{\mathrm{54}\sqrt{\mathrm{3}}−\mathrm{41}\sqrt{\mathrm{5}}}}{\:\sqrt{\mathrm{3}}} \\ $$$$\mathrm{or},\:\mathrm{A}=\frac{\sqrt[{\mathrm{3}}]{\mathrm{54}\sqrt{\mathrm{3}}+\mathrm{41}\sqrt{\mathrm{5}}+\mathrm{54}\sqrt{\mathrm{3}}−\mathrm{41}\sqrt{\mathrm{5}}}}{\:\sqrt{\mathrm{3}}} \\ $$$$\mathrm{or},\:\mathrm{A}=\frac{\sqrt[{\mathrm{3}}]{\mathrm{54}\sqrt{\mathrm{3}}+\mathrm{54}\sqrt{\mathrm{3}}}}{\:\sqrt{\mathrm{3}}} \\ $$$$\mathrm{or},\:\mathrm{A}=\frac{\sqrt[{\mathrm{3}}]{\mathrm{2}×\mathrm{54}\sqrt{\mathrm{3}}}}{\:\sqrt{\mathrm{3}}} \\ $$$$\mathrm{or},\:\mathrm{A}=\frac{\sqrt[{\mathrm{3}}]{\mathrm{108}\sqrt{\mathrm{3}}}}{\:\sqrt{\mathrm{3}}} \\ $$$$\mathrm{or},\:\mathrm{A}=\frac{\sqrt[{\mathrm{3}}]{\mathrm{3}×\mathrm{3}×\mathrm{3}×\mathrm{4}\sqrt{\mathrm{3}}}}{\:\sqrt{\mathrm{3}}} \\ $$$$\mathrm{or},\:\mathrm{A}=\frac{\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{4}\sqrt{\mathrm{3}}}}{\:\sqrt{\mathrm{3}}}×\frac{\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{3}}} \\ $$$$\mathrm{or},\:\mathrm{A}=\frac{\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{4}\sqrt{\mathrm{3}}}×\sqrt{\mathrm{3}}}{\:\mathrm{3}} \\ $$$$\mathrm{or},\:\mathrm{A}=\sqrt[{\mathrm{3}}]{\mathrm{2}^{\mathrm{2}} \sqrt{\mathrm{3}}}×\sqrt{\mathrm{3}} \\ $$$$\mathrm{or},\:\mathrm{A}=\sqrt[{\mathrm{3}}]{\sqrt{\mathrm{6}}}×\sqrt{\mathrm{3}} \\ $$$$\mathrm{or},\:\mathrm{A}=\sqrt[{\mathrm{6}}]{\mathrm{6}}×\sqrt{\mathrm{3}} \\ $$$$\mathrm{or},\:\mathrm{A}=\mathrm{1}.\mathrm{34}×\mathrm{1}.\mathrm{73}=\mathrm{2}.\mathrm{3} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *