Menu Close

Question-122431

Tinku Tara 0 Comments
Pin




Question Number 122431 by danielasebhofoh last updated on 17/Nov/20
Answered by mindispower last updated on 18/Nov/20
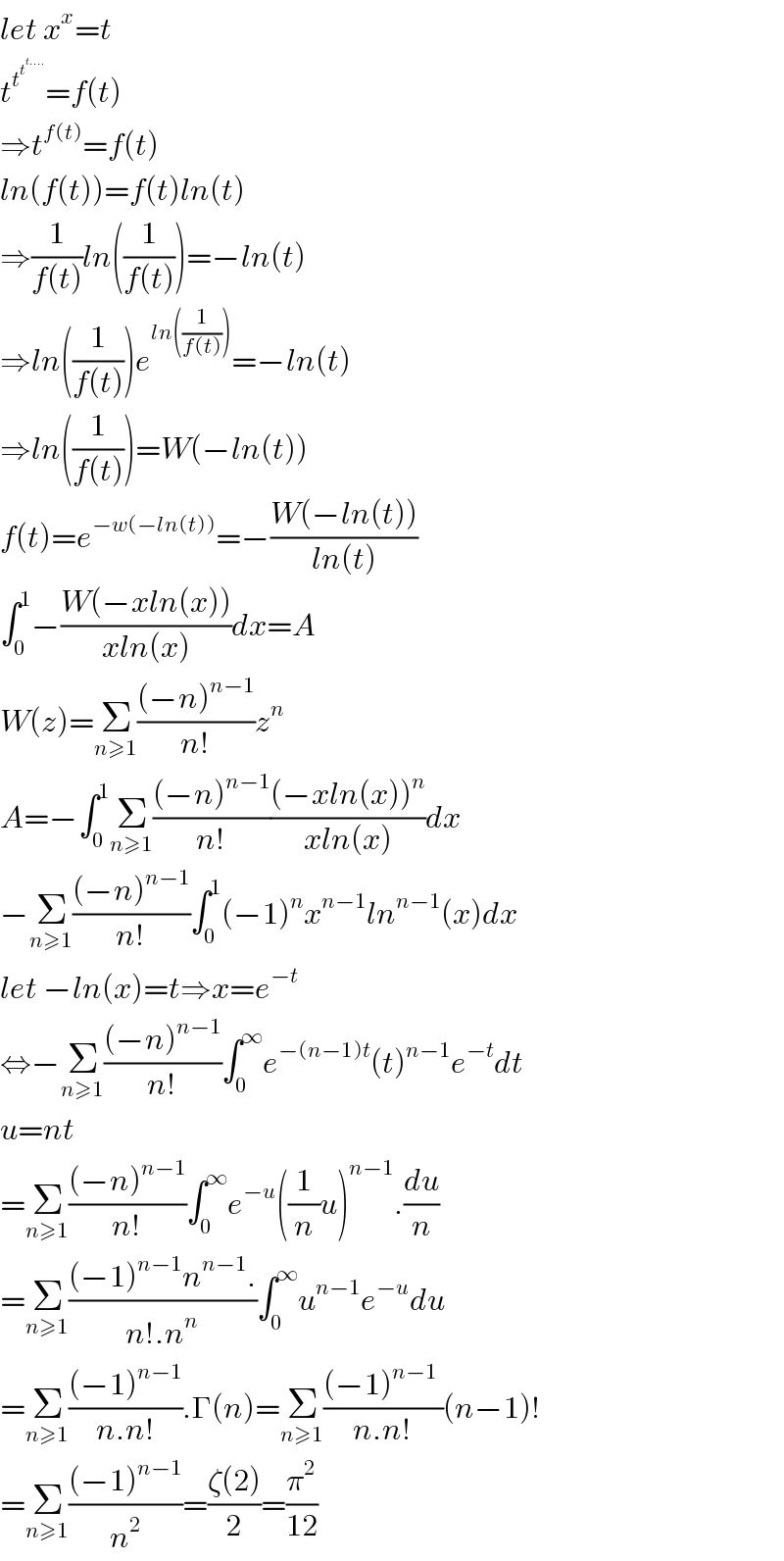
let x^x =t t^t^t^(t....) =f(t) ⇒t^(f(t)) =f(t) ln(f(t))=f(t)ln(t) ⇒(1/(f(t)))ln((1/(f(t))))=−ln(t) ⇒ln((1/(f(t))))e^(ln((1/(f(t))))) =−ln(t) ⇒ln((1/(f(t))))=W(−ln(t)) f(t)=e^(−w(−ln(t))) =−((W(−ln(t)))/(ln(t))) ∫_0 ^1 −((W(−xln(x)))/(xln(x)))dx=A W(z)=Σ_(n≥1) (((−n)^(n−1) )/(n!))z^n A=−∫_0 ^1 Σ_(n≥1) (((−n)^(n−1) )/(n!))(((−xln(x))^n )/(xln(x)))dx −Σ_(n≥1) (((−n)^(n−1) )/(n!))∫_0 ^1 (−1)^n x^(n−1) ln^(n−1) (x)dx let −ln(x)=t⇒x=e^(−t) ⇔−Σ_(n≥1) (((−n)^(n−1) )/(n!))∫_0 ^∞ e^(−(n−1)t) (t)^(n−1) e^(−t) dt u=nt =Σ_(n≥1) (((−n)^(n−1) )/(n!))∫_0 ^∞ e^(−u) ((1/n)u)^(n−1) .(du/n) =Σ_(n≥1) (((−1)^(n−1) n^(n−1) .)/(n!.n^n ))∫_0 ^∞ u^(n−1) e^(−u) du =Σ_(n≥1) (((−1)^(n−1) )/(n.n!)).Γ(n)=Σ_(n≥1) (((−1)^(n−1) )/(n.n!))(n−1)! =Σ_(n≥1) (((−1)^(n−1) )/n^2 )=((ζ(2))/2)=(π^2 /(12))
$${let}\:{x}^{{x}} ={t} \\ $$$${t}^{{t}^{{t}^{{t}….} } } ={f}\left({t}\right) \\ $$$$\Rightarrow{t}^{{f}\left({t}\right)} ={f}\left({t}\right) \\ $$$${ln}\left({f}\left({t}\right)\right)={f}\left({t}\right){ln}\left({t}\right) \\ $$$$\Rightarrow\frac{\mathrm{1}}{{f}\left({t}\right)}{ln}\left(\frac{\mathrm{1}}{{f}\left({t}\right)}\right)=−{ln}\left({t}\right) \\ $$$$\Rightarrow{ln}\left(\frac{\mathrm{1}}{{f}\left({t}\right)}\right){e}^{{ln}\left(\frac{\mathrm{1}}{{f}\left({t}\right)}\right)} =−{ln}\left({t}\right) \\ $$$$\Rightarrow{ln}\left(\frac{\mathrm{1}}{{f}\left({t}\right)}\right)={W}\left(−{ln}\left({t}\right)\right) \\ $$$${f}\left({t}\right)={e}^{−{w}\left(−{ln}\left({t}\right)\right)} =−\frac{{W}\left(−{ln}\left({t}\right)\right)}{{ln}\left({t}\right)} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} −\frac{{W}\left(−{xln}\left({x}\right)\right)}{{xln}\left({x}\right)}{dx}={A} \\ $$$${W}\left({z}\right)=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left(−{n}\right)^{{n}−\mathrm{1}} }{{n}!}{z}^{{n}} \\ $$$${A}=−\int_{\mathrm{0}} ^{\mathrm{1}} \underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left(−{n}\right)^{{n}−\mathrm{1}} }{{n}!}\frac{\left(−{xln}\left({x}\right)\right)^{{n}} }{{xln}\left({x}\right)}{dx} \\ $$$$−\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left(−{n}\right)^{{n}−\mathrm{1}} }{{n}!}\int_{\mathrm{0}} ^{\mathrm{1}} \left(−\mathrm{1}\right)^{{n}} {x}^{{n}−\mathrm{1}} {ln}^{{n}−\mathrm{1}} \left({x}\right){dx} \\ $$$${let}\:−{ln}\left({x}\right)={t}\Rightarrow{x}={e}^{−{t}} \\ $$$$\Leftrightarrow−\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left(−{n}\right)^{{n}−\mathrm{1}} }{{n}!}\int_{\mathrm{0}} ^{\infty} {e}^{−\left({n}−\mathrm{1}\right){t}} \left({t}\right)^{{n}−\mathrm{1}} {e}^{−{t}} {dt} \\ $$$${u}={nt} \\ $$$$=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left(−{n}\right)^{{n}−\mathrm{1}} }{{n}!}\int_{\mathrm{0}} ^{\infty} {e}^{−{u}} \left(\frac{\mathrm{1}}{{n}}{u}\right)^{{n}−\mathrm{1}} .\frac{{du}}{{n}} \\ $$$$=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} {n}^{{n}−\mathrm{1}} .}{{n}!.{n}^{{n}} }\int_{\mathrm{0}} ^{\infty} {u}^{{n}−\mathrm{1}} {e}^{−{u}} {du} \\ $$$$=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}.{n}!}.\Gamma\left({n}\right)=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \:}{{n}.{n}!}\left({n}−\mathrm{1}\right)! \\ $$$$=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}^{\mathrm{2}} }=\frac{\zeta\left(\mathrm{2}\right)}{\mathrm{2}}=\frac{\pi^{\mathrm{2}} }{\mathrm{12}} \\ $$
Commented by hatakekakashi1729gmailcom last updated on 30/Nov/20
let x^x =t t^t^t^(t....) =f(t) ⇒t^(f(t)) =f(t) ln(f(t))=f(t)ln(t) ⇒(1/(f(t)))ln((1/(f(t))))=−ln(t) ⇒ln((1/(f(t))))e^(ln((1/(f(t))))) =−ln(t) ⇒ln((1/(f(t))))=W(−ln(t))??????? f(t)=e^(−w(−ln(t))) =−((W(−ln(t)))/(ln(t))) ∫_0 ^1 −((W(−xln(x)))/(xln(x)))dx=A W(z)=Σ_(n≥1) (((−n)^(n−1) )/(n!))z^n ???????????? A=−∫_0 ^1 Σ_(n≥1) (((−n)^(n−1) )/(n!))(((−xln(x))^n )/(xln(x)))dx −Σ_(n≥1) (((−n)^(n−1) )/(n!))∫_0 ^1 (−1)^n x^(n−1) ln^(n−1) (x)dx let −ln(x)=t⇒x=e^(−t) ⇔−Σ_(n≥1) (((−n)^(n−1) )/(n!))∫_0 ^∞ e^(−(n−1)t) (t)^(n−1) e^(−t) dt u=nt =Σ_(n≥1) (((−n)^(n−1) )/(n!))∫_0 ^∞ e^(−u) ((1/n)u)^(n−1) .(du/n) =Σ_(n≥1) (((−1)^(n−1) n^(n−1) .)/(n!.n^n ))∫_0 ^∞ u^(n−1) e^(−u) du =Σ_(n≥1) (((−1)^(n−1) )/(n.n!)).Γ(n)=Σ_(n≥1) (((−1)^(n−1) )/(n.n!))(n−1)! =Σ_(n≥1) (((−1)^(n−1) )/n^2 )=((ζ(2))/2)=(π^2 /(12))
$${let}\:{x}^{{x}} ={t} \\ $$$${t}^{{t}^{{t}^{{t}….} } } ={f}\left({t}\right) \\ $$$$\Rightarrow{t}^{{f}\left({t}\right)} ={f}\left({t}\right) \\ $$$${ln}\left({f}\left({t}\right)\right)={f}\left({t}\right){ln}\left({t}\right) \\ $$$$\Rightarrow\frac{\mathrm{1}}{{f}\left({t}\right)}{ln}\left(\frac{\mathrm{1}}{{f}\left({t}\right)}\right)=−{ln}\left({t}\right) \\ $$$$\Rightarrow{ln}\left(\frac{\mathrm{1}}{{f}\left({t}\right)}\right){e}^{{ln}\left(\frac{\mathrm{1}}{{f}\left({t}\right)}\right)} =−{ln}\left({t}\right) \\ $$$$\Rightarrow{ln}\left(\frac{\mathrm{1}}{{f}\left({t}\right)}\right)={W}\left(−{ln}\left({t}\right)\right)??????? \\ $$$${f}\left({t}\right)={e}^{−{w}\left(−{ln}\left({t}\right)\right)} =−\frac{{W}\left(−{ln}\left({t}\right)\right)}{{ln}\left({t}\right)} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} −\frac{{W}\left(−{xln}\left({x}\right)\right)}{{xln}\left({x}\right)}{dx}={A} \\ $$$${W}\left({z}\right)=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left(−{n}\right)^{{n}−\mathrm{1}} }{{n}!}{z}^{{n}} ???????????? \\ $$$${A}=−\int_{\mathrm{0}} ^{\mathrm{1}} \underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left(−{n}\right)^{{n}−\mathrm{1}} }{{n}!}\frac{\left(−{xln}\left({x}\right)\right)^{{n}} }{{xln}\left({x}\right)}{dx} \\ $$$$−\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left(−{n}\right)^{{n}−\mathrm{1}} }{{n}!}\int_{\mathrm{0}} ^{\mathrm{1}} \left(−\mathrm{1}\right)^{{n}} {x}^{{n}−\mathrm{1}} {ln}^{{n}−\mathrm{1}} \left({x}\right){dx} \\ $$$${let}\:−{ln}\left({x}\right)={t}\Rightarrow{x}={e}^{−{t}} \\ $$$$\Leftrightarrow−\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left(−{n}\right)^{{n}−\mathrm{1}} }{{n}!}\int_{\mathrm{0}} ^{\infty} {e}^{−\left({n}−\mathrm{1}\right){t}} \left({t}\right)^{{n}−\mathrm{1}} {e}^{−{t}} {dt} \\ $$$${u}={nt} \\ $$$$=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left(−{n}\right)^{{n}−\mathrm{1}} }{{n}!}\int_{\mathrm{0}} ^{\infty} {e}^{−{u}} \left(\frac{\mathrm{1}}{{n}}{u}\right)^{{n}−\mathrm{1}} .\frac{{du}}{{n}} \\ $$$$=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} {n}^{{n}−\mathrm{1}} .}{{n}!.{n}^{{n}} }\int_{\mathrm{0}} ^{\infty} {u}^{{n}−\mathrm{1}} {e}^{−{u}} {du} \\ $$$$=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}.{n}!}.\Gamma\left({n}\right)=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \:}{{n}.{n}!}\left({n}−\mathrm{1}\right)! \\ $$$$=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}^{\mathrm{2}} }=\frac{\zeta\left(\mathrm{2}\right)}{\mathrm{2}}=\frac{\pi^{\mathrm{2}} }{\mathrm{12}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *