Menu Close

Question-122443

Tinku Tara 0 Comments
Pin




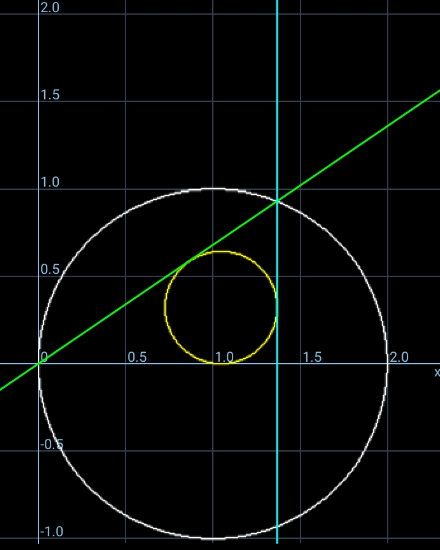
Question Number 122443 by ajfour last updated on 17/Nov/20
Commented by ajfour last updated on 17/Nov/20
Find ((r/R))_(max) .
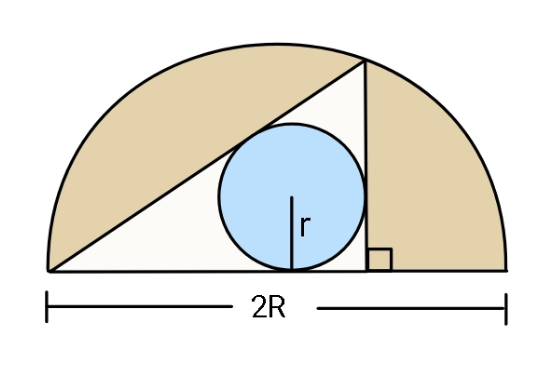
$${Find}\:\left(\frac{{r}}{{R}}\right)_{{max}} . \\ $$
Answered by ajfour last updated on 17/Nov/20
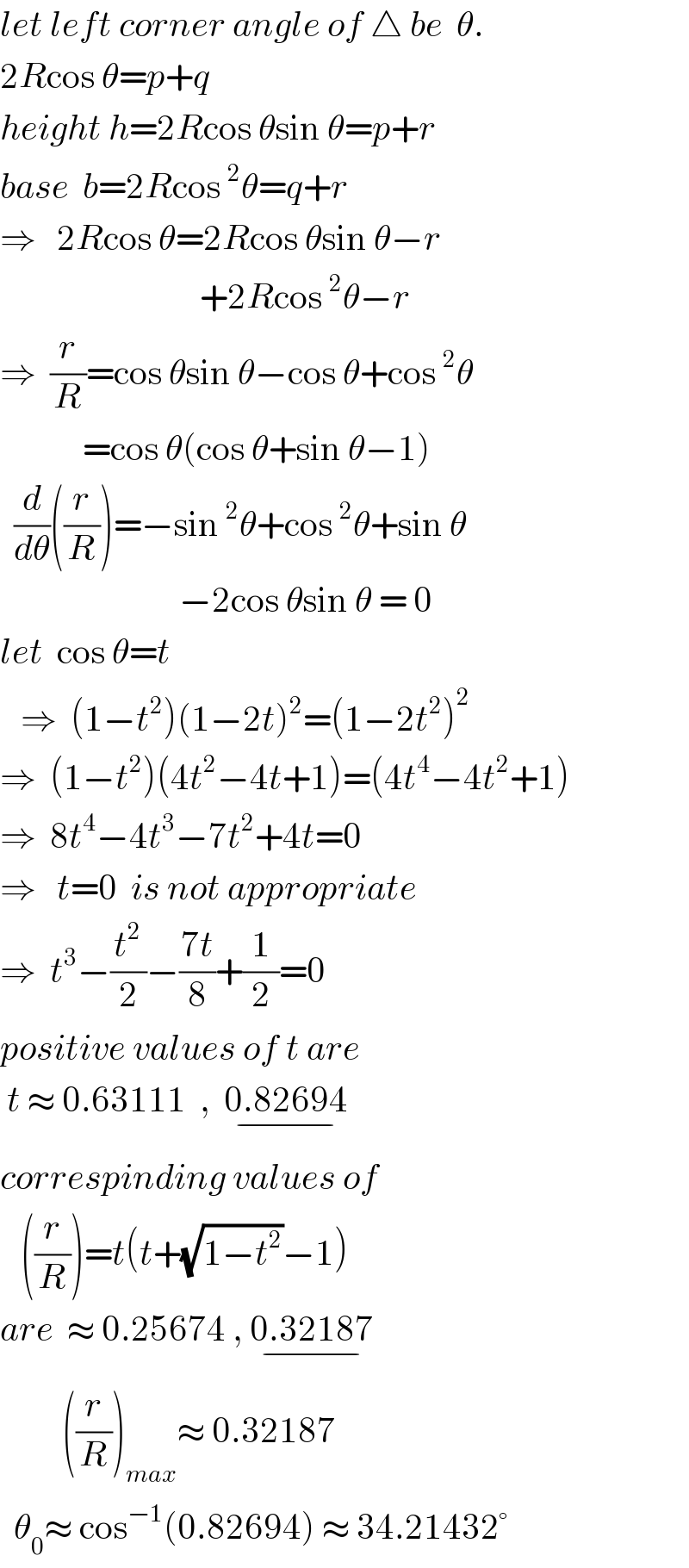
let left corner angle of △ be θ. 2Rcos θ=p+q height h=2Rcos θsin θ=p+r base b=2Rcos^2 θ=q+r ⇒ 2Rcos θ=2Rcos θsin θ−r +2Rcos^2 θ−r ⇒ (r/R)=cos θsin θ−cos θ+cos^2 θ =cos θ(cos θ+sin θ−1) (d/dθ)((r/R))=−sin^2 θ+cos^2 θ+sin θ −2cos θsin θ = 0 let cos θ=t ⇒ (1−t^2 )(1−2t)^2 =(1−2t^2 )^2 ⇒ (1−t^2 )(4t^2 −4t+1)=(4t^4 −4t^2 +1) ⇒ 8t^4 −4t^3 −7t^2 +4t=0 ⇒ t=0 is not appropriate ⇒ t^3 −(t^2 /2)−((7t)/8)+(1/2)=0 positive values of t are t ≈ 0.63111 , 0.82694_(−) correspinding values of ((r/R))=t(t+(√(1−t^2 ))−1) are ≈ 0.25674 , 0.32187_(−) ((r/R))_(max) ≈ 0.32187 θ_0 ≈ cos^(−1) (0.82694) ≈ 34.21432°
$${let}\:{left}\:{corner}\:{angle}\:{of}\:\bigtriangleup\:{be}\:\:\theta. \\ $$$$\mathrm{2}{R}\mathrm{cos}\:\theta={p}+{q} \\ $$$${height}\:{h}=\mathrm{2}{R}\mathrm{cos}\:\theta\mathrm{sin}\:\theta={p}+{r} \\ $$$${base}\:\:{b}=\mathrm{2}{R}\mathrm{cos}\:^{\mathrm{2}} \theta={q}+{r} \\ $$$$\Rightarrow\:\:\:\mathrm{2}{R}\mathrm{cos}\:\theta=\mathrm{2}{R}\mathrm{cos}\:\theta\mathrm{sin}\:\theta−{r} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{2}{R}\mathrm{cos}\:^{\mathrm{2}} \theta−{r} \\ $$$$\Rightarrow\:\:\frac{{r}}{{R}}=\mathrm{cos}\:\theta\mathrm{sin}\:\theta−\mathrm{cos}\:\theta+\mathrm{cos}\:^{\mathrm{2}} \theta \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{cos}\:\theta\left(\mathrm{cos}\:\theta+\mathrm{sin}\:\theta−\mathrm{1}\right)\:\:\:\: \\ $$$$\:\:\frac{{d}}{{d}\theta}\left(\frac{{r}}{{R}}\right)=−\mathrm{sin}\:^{\mathrm{2}} \theta+\mathrm{cos}\:^{\mathrm{2}} \theta+\mathrm{sin}\:\theta \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{2cos}\:\theta\mathrm{sin}\:\theta\:=\:\mathrm{0} \\ $$$${let}\:\:\mathrm{cos}\:\theta={t}\:\:\: \\ $$$$\:\:\:\Rightarrow\:\:\left(\mathrm{1}−{t}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{2}{t}\right)^{\mathrm{2}} =\left(\mathrm{1}−\mathrm{2}{t}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\left(\mathrm{1}−{t}^{\mathrm{2}} \right)\left(\mathrm{4}{t}^{\mathrm{2}} −\mathrm{4}{t}+\mathrm{1}\right)=\left(\mathrm{4}{t}^{\mathrm{4}} −\mathrm{4}{t}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$$\Rightarrow\:\:\mathrm{8}{t}^{\mathrm{4}} −\mathrm{4}{t}^{\mathrm{3}} −\mathrm{7}{t}^{\mathrm{2}} +\mathrm{4}{t}=\mathrm{0} \\ $$$$\Rightarrow\:\:\:{t}=\mathrm{0}\:\:{is}\:{not}\:{appropriate} \\ $$$$\Rightarrow\:\:{t}^{\mathrm{3}} −\frac{{t}^{\mathrm{2}} }{\mathrm{2}}−\frac{\mathrm{7}{t}}{\mathrm{8}}+\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{0} \\ $$$${positive}\:{values}\:{of}\:{t}\:{are} \\ $$$$\:{t}\:\approx\:\mathrm{0}.\mathrm{63111}\:\:,\:\:\underset{−} {\mathrm{0}.\mathrm{82694}} \\ $$$${correspinding}\:{values}\:{of} \\ $$$$\:\:\:\left(\frac{{r}}{{R}}\right)={t}\left({t}+\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }−\mathrm{1}\right) \\ $$$${are}\:\:\approx\:\mathrm{0}.\mathrm{25674}\:,\:\underset{−} {\mathrm{0}.\mathrm{32187}} \\ $$$$\:\:\:\:\:\:\:\:\:\left(\frac{{r}}{{R}}\right)_{{max}} \approx\:\mathrm{0}.\mathrm{32187} \\ $$$$\:\:\theta_{\mathrm{0}} \approx\:\mathrm{cos}^{−\mathrm{1}} \left(\mathrm{0}.\mathrm{82694}\right)\:\approx\:\mathrm{34}.\mathrm{21432}° \\ $$
Commented by ajfour last updated on 17/Nov/20

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *