Menu Close

Question-122445

Tinku Tara 0 Comments
Pin




Question Number 122445 by benjo_mathlover last updated on 17/Nov/20
Answered by TANMAY PANACEA last updated on 17/Nov/20
using Titu lemma (1^2 /x)+(3^2 /y)+(5^2 /z)≥(((1+3+5)^2 )/(x+y+z)) (1^2 /x)+(3^2 /y)+(5^2 /z)≥81
$${using}\:{Titu}\:{lemma} \\ $$$$\frac{\mathrm{1}^{\mathrm{2}} }{{x}}+\frac{\mathrm{3}^{\mathrm{2}} }{{y}}+\frac{\mathrm{5}^{\mathrm{2}} }{{z}}\geqslant\frac{\left(\mathrm{1}+\mathrm{3}+\mathrm{5}\right)^{\mathrm{2}} }{{x}+{y}+{z}} \\ $$$$\frac{\mathrm{1}^{\mathrm{2}} }{{x}}+\frac{\mathrm{3}^{\mathrm{2}} }{{y}}+\frac{\mathrm{5}^{\mathrm{2}} }{{z}}\geqslant\mathrm{81} \\ $$
Commented by TANMAY PANACEA last updated on 17/Nov/20
Commented by rs4089 last updated on 18/Nov/20
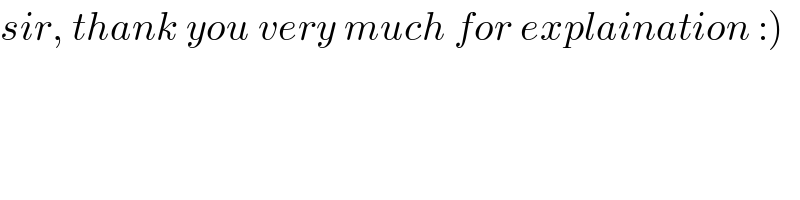
sir, thank you very much for explaination :)
$$\left.{sir},\:{thank}\:{you}\:{very}\:{much}\:{for}\:{explaination}\::\right) \\ $$
Answered by Olaf last updated on 17/Nov/20
1) 1st method : Let f(x,y) = (1/x)+(9/y)+((25)/z) with z = 1−x−y ⇒ f(x,y) = (1/x)+(9/y)+((25)/(1−x−y)) (∂f/∂x)(x,y) = −(1/x^2 )+((25)/((1−x−y)^2 )) (∂f/∂y)(x,y) = −(9/y^2 )+((25)/((1−x−y)^2 )) We solve : { (((∂f/∂x)(x,y) = 0 = −(1/x^2 )+((25)/((1−x−y)^2 )) (1))),(((∂f/∂y)(x,y) = 0 = −(9/y^2 )+((25)/((1−x−y)^2 )) (2))) :}_ (1)−(2) : y = ±3x but x>0, y>0 ⇒ y = 3x With (1) : −(1/x^2 )+((25)/((1−4x)^2 )) = 0 25x^2 −(1−4x)^2 = 0 9x^2 +8x−1 = 0 9(x+1)(x−(1/9)) = 0 x>0 ⇒ x = (1/9) ⇒ y = (1/3) ⇒ z = (5/9) ⇒ f(x,y,z) = f((1/9),(1/3),(5/9)) = (1/(1/9))+(9/(1/3))+((25)/(5/9)) = 81 2) 2nd method The function is symmetric with respect to x, y = 3x, z = 5x ⇒ x+y+z = 1 = 9x We find x = (1/9) etc... 3) 3rd method Let f(x,y,z) = (1/x)+(9/y)+((25)/z) Let the constraint c(x,y,z) = x+y+z−1 = 0 Let g(x,y,z,λ) = f(x,y,z)+λc(x,y,z) (∂g/∂x)(x,y,z,λ) = −(1/x^2 )+λ (∂g/∂y)(x,y,z,λ) = −(9/y^2 )+λ (∂g/∂z)(x,y,z,λ) = −((25)/z^2 )+λ (∂g/∂λ)(x,y,z,λ) = x+y+z−1 (∂g/∂x)(x,y,z,λ) = 0 ⇒ x = (1/( (√λ))) (∂g/∂y)(x,y,z,λ) = 0 ⇒ y = (3/( (√λ))) (∂g/∂z)(x,y,z,λ) = 0 ⇒ z = (5/( (√λ))) (∂g/∂λ)(x,y,z,λ) = 0 ⇒ (1/( (√λ)))+(3/( (√λ)))+(5/( (√λ)))−1 = 0 ⇒ (1/( (√λ))) = (1/9) ⇒ x = (1/9) ⇒ y = (1/3) ⇒z = (5/9)
$$\left.\mathrm{1}\right)\:\mathrm{1st}\:\mathrm{method}\:: \\ $$$$\mathrm{Let}\:{f}\left({x},{y}\right)\:=\:\frac{\mathrm{1}}{{x}}+\frac{\mathrm{9}}{{y}}+\frac{\mathrm{25}}{{z}} \\ $$$$\mathrm{with}\:{z}\:=\:\mathrm{1}−{x}−{y} \\ $$$$\Rightarrow\:{f}\left({x},{y}\right)\:=\:\frac{\mathrm{1}}{{x}}+\frac{\mathrm{9}}{{y}}+\frac{\mathrm{25}}{\mathrm{1}−{x}−{y}} \\ $$$$\frac{\partial{f}}{\partial{x}}\left({x},{y}\right)\:=\:−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\frac{\mathrm{25}}{\left(\mathrm{1}−{x}−{y}\right)^{\mathrm{2}} } \\ $$$$\frac{\partial{f}}{\partial{y}}\left({x},{y}\right)\:=\:−\frac{\mathrm{9}}{{y}^{\mathrm{2}} }+\frac{\mathrm{25}}{\left(\mathrm{1}−{x}−{y}\right)^{\mathrm{2}} } \\ $$$$\mathrm{We}\:\mathrm{solve}\:: \\ $$$$\begin{cases}{\frac{\partial{f}}{\partial{x}}\left({x},{y}\right)\:=\:\mathrm{0}\:=\:−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\frac{\mathrm{25}}{\left(\mathrm{1}−{x}−{y}\right)^{\mathrm{2}} }\:\left(\mathrm{1}\right)}\\{\frac{\partial{f}}{\partial{y}}\left({x},{y}\right)\:=\:\mathrm{0}\:=\:−\frac{\mathrm{9}}{{y}^{\mathrm{2}} }+\frac{\mathrm{25}}{\left(\mathrm{1}−{x}−{y}\right)^{\mathrm{2}} }\:\left(\mathrm{2}\right)}\end{cases}_{} \\ $$$$\left(\mathrm{1}\right)−\left(\mathrm{2}\right)\::\:{y}\:=\:\pm\mathrm{3}{x} \\ $$$$\mathrm{but}\:{x}>\mathrm{0},\:{y}>\mathrm{0}\:\Rightarrow\:{y}\:=\:\mathrm{3}{x} \\ $$$$\mathrm{With}\:\left(\mathrm{1}\right)\:: \\ $$$$−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\frac{\mathrm{25}}{\left(\mathrm{1}−\mathrm{4}{x}\right)^{\mathrm{2}} }\:=\:\mathrm{0} \\ $$$$\mathrm{25}{x}^{\mathrm{2}} −\left(\mathrm{1}−\mathrm{4}{x}\right)^{\mathrm{2}} \:=\:\mathrm{0} \\ $$$$\mathrm{9}{x}^{\mathrm{2}} +\mathrm{8}{x}−\mathrm{1}\:=\:\mathrm{0} \\ $$$$\mathrm{9}\left({x}+\mathrm{1}\right)\left({x}−\frac{\mathrm{1}}{\mathrm{9}}\right)\:=\:\mathrm{0} \\ $$$${x}>\mathrm{0}\:\Rightarrow\:{x}\:=\:\frac{\mathrm{1}}{\mathrm{9}}\:\Rightarrow\:{y}\:=\:\frac{\mathrm{1}}{\mathrm{3}}\:\Rightarrow\:{z}\:=\:\frac{\mathrm{5}}{\mathrm{9}} \\ $$$$\Rightarrow\:{f}\left({x},{y},{z}\right)\:=\:{f}\left(\frac{\mathrm{1}}{\mathrm{9}},\frac{\mathrm{1}}{\mathrm{3}},\frac{\mathrm{5}}{\mathrm{9}}\right)\:=\:\frac{\mathrm{1}}{\mathrm{1}/\mathrm{9}}+\frac{\mathrm{9}}{\mathrm{1}/\mathrm{3}}+\frac{\mathrm{25}}{\mathrm{5}/\mathrm{9}}\:=\:\mathrm{81} \\ $$$$\left.\mathrm{2}\right)\:\mathrm{2nd}\:\mathrm{method} \\ $$$$\mathrm{The}\:\mathrm{function}\:\mathrm{is}\:\mathrm{symmetric}\:\mathrm{with}\:\mathrm{respect} \\ $$$$\mathrm{to}\:{x},\:{y}\:=\:\mathrm{3}{x},\:{z}\:=\:\mathrm{5}{x} \\ $$$$\Rightarrow\:{x}+{y}+{z}\:=\:\mathrm{1}\:=\:\mathrm{9}{x} \\ $$$$\mathrm{We}\:\mathrm{find}\:{x}\:=\:\frac{\mathrm{1}}{\mathrm{9}}\:\mathrm{etc}… \\ $$$$\left.\mathrm{3}\right)\:\mathrm{3rd}\:\mathrm{method} \\ $$$$\mathrm{Let}\:{f}\left({x},{y},{z}\right)\:=\:\frac{\mathrm{1}}{{x}}+\frac{\mathrm{9}}{{y}}+\frac{\mathrm{25}}{{z}} \\ $$$$\mathrm{Let}\:\mathrm{the}\:\mathrm{constraint}\:{c}\left({x},{y},{z}\right)\:=\:{x}+{y}+{z}−\mathrm{1}\:=\:\mathrm{0} \\ $$$$\mathrm{Let}\:{g}\left({x},{y},{z},\lambda\right)\:=\:{f}\left({x},{y},{z}\right)+\lambda{c}\left({x},{y},{z}\right) \\ $$$$\frac{\partial{g}}{\partial{x}}\left({x},{y},{z},\lambda\right)\:=\:−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\lambda \\ $$$$\frac{\partial{g}}{\partial{y}}\left({x},{y},{z},\lambda\right)\:=\:−\frac{\mathrm{9}}{{y}^{\mathrm{2}} }+\lambda \\ $$$$\frac{\partial{g}}{\partial{z}}\left({x},{y},{z},\lambda\right)\:=\:−\frac{\mathrm{25}}{{z}^{\mathrm{2}} }+\lambda \\ $$$$\frac{\partial{g}}{\partial\lambda}\left({x},{y},{z},\lambda\right)\:=\:{x}+{y}+{z}−\mathrm{1} \\ $$$$\frac{\partial{g}}{\partial{x}}\left({x},{y},{z},\lambda\right)\:=\:\mathrm{0}\:\Rightarrow\:{x}\:=\:\frac{\mathrm{1}}{\:\sqrt{\lambda}} \\ $$$$\frac{\partial{g}}{\partial{y}}\left({x},{y},{z},\lambda\right)\:=\:\mathrm{0}\:\Rightarrow\:{y}\:=\:\frac{\mathrm{3}}{\:\sqrt{\lambda}} \\ $$$$\frac{\partial{g}}{\partial{z}}\left({x},{y},{z},\lambda\right)\:=\:\mathrm{0}\:\Rightarrow\:{z}\:=\:\frac{\mathrm{5}}{\:\sqrt{\lambda}} \\ $$$$\frac{\partial{g}}{\partial\lambda}\left({x},{y},{z},\lambda\right)\:=\:\mathrm{0}\:\Rightarrow\:\frac{\mathrm{1}}{\:\sqrt{\lambda}}+\frac{\mathrm{3}}{\:\sqrt{\lambda}}+\frac{\mathrm{5}}{\:\sqrt{\lambda}}−\mathrm{1}\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\frac{\mathrm{1}}{\:\sqrt{\lambda}}\:=\:\frac{\mathrm{1}}{\mathrm{9}}\:\Rightarrow\:{x}\:=\:\frac{\mathrm{1}}{\mathrm{9}}\:\Rightarrow\:{y}\:=\:\frac{\mathrm{1}}{\mathrm{3}}\:\Rightarrow{z}\:=\:\frac{\mathrm{5}}{\mathrm{9}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *