Question-122469

Question Number 122469 by benjo_mathlover last updated on 17/Nov/20

Commented by benjo_mathlover last updated on 17/Nov/20

i′m forgot the formula the average rate of change of the function. is it A(x) = (1/(b−a)) ∫_a ^b f(x) dx ?

$${i}'{m}\:{forgot}\:{the}\:{formula}\:{the}\:\:{average}\:{rate}\:{of} \\ $$$${change}\:{of}\:{the}\:{function}.\:{is}\:{it}\: \\ $$$${A}\left({x}\right)\:=\:\frac{\mathrm{1}}{{b}−{a}}\:\underset{{a}} {\overset{{b}} {\int}}\:{f}\left({x}\right)\:{dx}\:? \\ $$

Commented by benjo_mathlover last updated on 17/Nov/20

$${prof}\:{Mjs},\:{mr}\:{W},\:{liberty}\:{and}\:{other}\:{can}\:{you} \\ $$$${help}\:{me} \\ $$

Commented by benjo_mathlover last updated on 17/Nov/20

The average rate of change of the function f(x)=∫_0 ^x (√(1+cos (t^2 ))) dt over the interval [1,3] is nearest to ...

$${The}\:{average}\:{rate}\:{of}\:{change}\:{of} \\ $$$${the}\:{function}\:{f}\left({x}\right)=\underset{\mathrm{0}} {\overset{{x}} {\int}}\:\sqrt{\mathrm{1}+\mathrm{cos}\:\left({t}^{\mathrm{2}} \right)}\:{dt}\: \\ $$$${over}\:{the}\:{interval}\:\left[\mathrm{1},\mathrm{3}\right]\:{is}\:{nearest} \\ $$$${to}\:… \\ $$

Commented by liberty last updated on 17/Nov/20

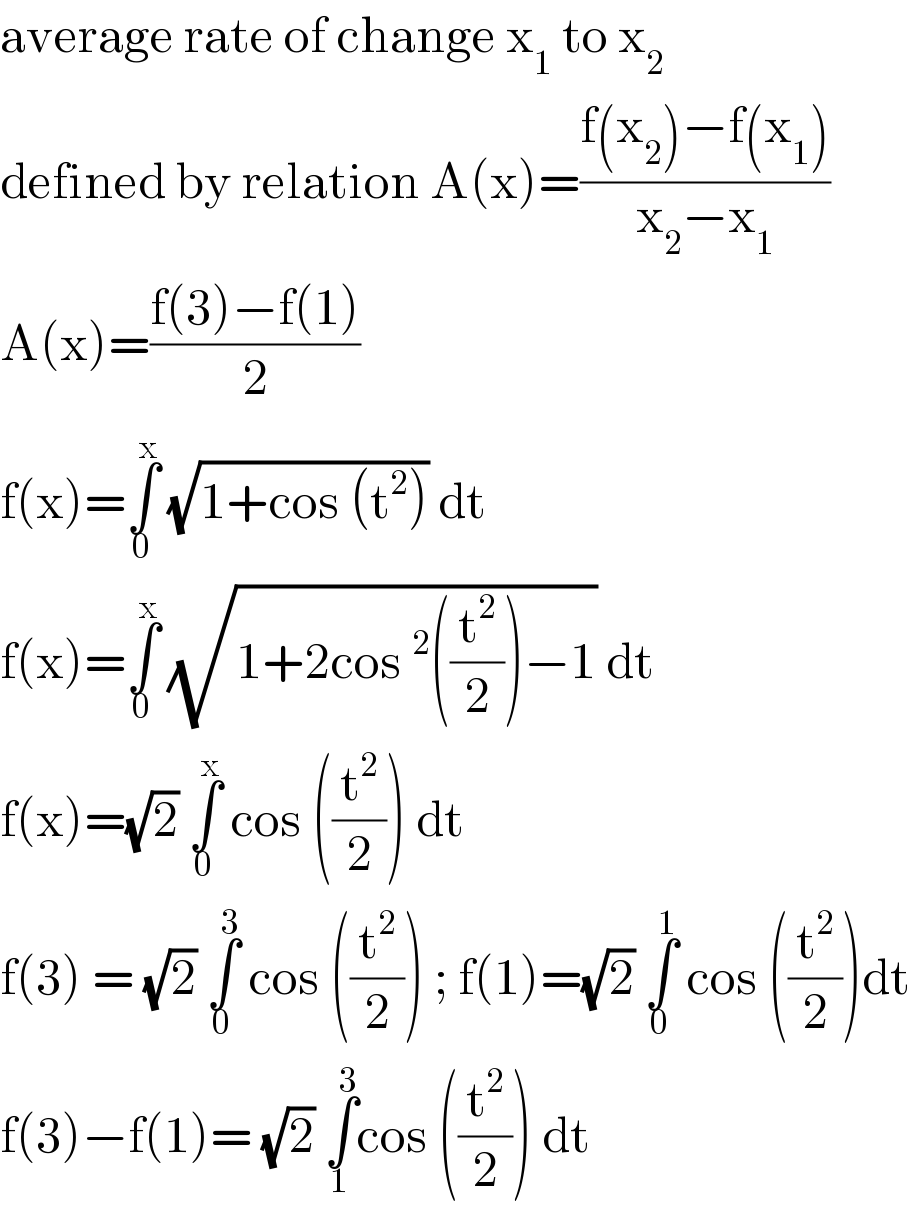
average rate of change x_1 to x_2 defined by relation A(x)=((f(x_2 )−f(x_1 ))/(x_2 −x_1 )) A(x)=((f(3)−f(1))/2) f(x)=∫_0 ^x (√(1+cos (t^2 ))) dt f(x)=∫_0 ^x (√(1+2cos^2 ((t^2 /2))−1)) dt f(x)=(√2) ∫_0 ^x cos ((t^2 /2)) dt f(3) = (√2) ∫_0 ^3 cos ((t^2 /2)) ; f(1)=(√2) ∫_0 ^1 cos ((t^2 /2))dt f(3)−f(1)= (√2) ∫_1 ^3 cos ((t^2 /2)) dt

$$\mathrm{average}\:\mathrm{rate}\:\mathrm{of}\:\mathrm{change}\:\mathrm{x}_{\mathrm{1}} \:\mathrm{to}\:\mathrm{x}_{\mathrm{2}} \\ $$$$\mathrm{defined}\:\mathrm{by}\:\mathrm{relation}\:\mathrm{A}\left(\mathrm{x}\right)=\frac{\mathrm{f}\left(\mathrm{x}_{\mathrm{2}} \right)−\mathrm{f}\left(\mathrm{x}_{\mathrm{1}} \right)}{\mathrm{x}_{\mathrm{2}} −\mathrm{x}_{\mathrm{1}} } \\ $$$$\mathrm{A}\left(\mathrm{x}\right)=\frac{\mathrm{f}\left(\mathrm{3}\right)−\mathrm{f}\left(\mathrm{1}\right)}{\mathrm{2}} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\underset{\mathrm{0}} {\overset{\mathrm{x}} {\int}}\:\sqrt{\mathrm{1}+\mathrm{cos}\:\left(\mathrm{t}^{\mathrm{2}} \right)}\:\mathrm{dt}\: \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\underset{\mathrm{0}} {\overset{\mathrm{x}} {\int}}\:\sqrt{\mathrm{1}+\mathrm{2cos}\:^{\mathrm{2}} \left(\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}\right)−\mathrm{1}}\:\mathrm{dt}\: \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\sqrt{\mathrm{2}}\:\underset{\mathrm{0}} {\overset{\mathrm{x}} {\int}}\:\mathrm{cos}\:\left(\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}\right)\:\mathrm{dt}\: \\ $$$$\mathrm{f}\left(\mathrm{3}\right)\:=\:\sqrt{\mathrm{2}}\:\underset{\mathrm{0}} {\overset{\mathrm{3}} {\int}}\:\mathrm{cos}\:\left(\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}\right)\:;\:\mathrm{f}\left(\mathrm{1}\right)=\sqrt{\mathrm{2}}\:\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\mathrm{cos}\:\left(\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}\right)\mathrm{dt} \\ $$$$\mathrm{f}\left(\mathrm{3}\right)−\mathrm{f}\left(\mathrm{1}\right)=\:\sqrt{\mathrm{2}}\:\underset{\mathrm{1}} {\overset{\mathrm{3}} {\int}}\mathrm{cos}\:\left(\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}\right)\:\mathrm{dt}\: \\ $$

Commented by mr W last updated on 17/Nov/20

A(x) = (1/(b−a)) ∫_a ^b f(x) dx is the average value of function f(x) in [a,b].

$${A}\left({x}\right)\:=\:\frac{\mathrm{1}}{{b}−{a}}\:\underset{{a}} {\overset{{b}} {\int}}\:{f}\left({x}\right)\:{dx} \\ $$$${is}\:{the}\:{average}\:{value}\:{of}\:{function}\:{f}\left({x}\right) \\ $$$${in}\:\left[{a},{b}\right]. \\ $$

Answered by liberty last updated on 18/Nov/20

Facebook Tweet Pin

Leave a Reply Cancel reply