Question Number 122505 by aupo14 last updated on 17/Nov/20
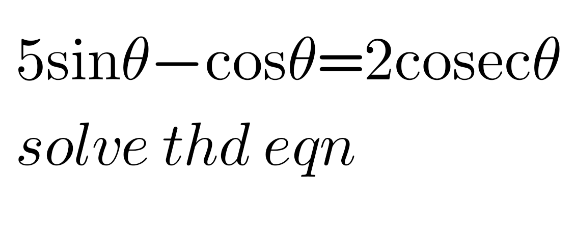
Answered by MJS_new last updated on 17/Nov/20
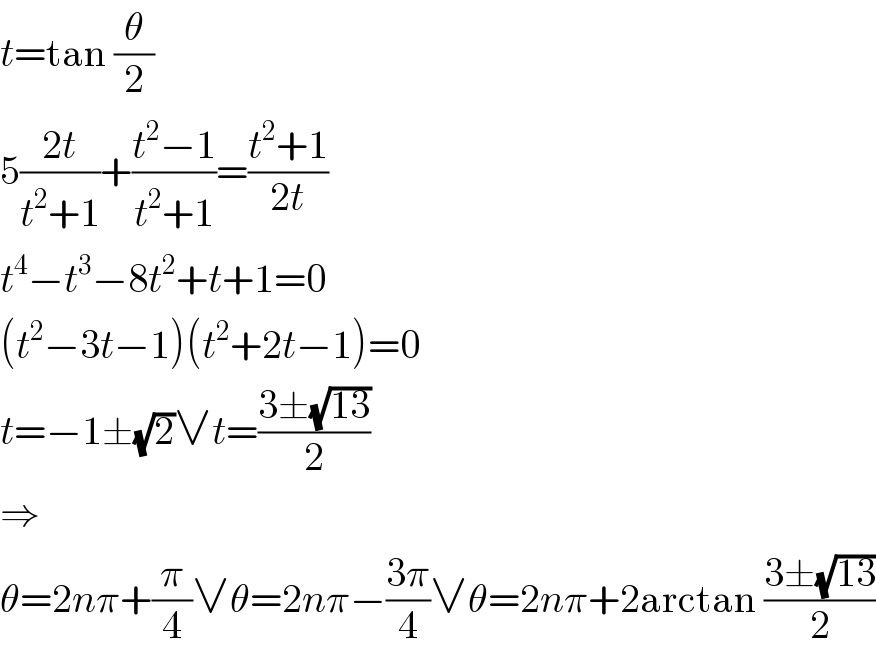
$${t}=\mathrm{tan}\:\frac{\theta}{\mathrm{2}} \\ $$$$\mathrm{5}\frac{\mathrm{2}{t}}{{t}^{\mathrm{2}} +\mathrm{1}}+\frac{{t}^{\mathrm{2}} −\mathrm{1}}{{t}^{\mathrm{2}} +\mathrm{1}}=\frac{{t}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}{t}} \\ $$$${t}^{\mathrm{4}} −{t}^{\mathrm{3}} −\mathrm{8}{t}^{\mathrm{2}} +{t}+\mathrm{1}=\mathrm{0} \\ $$$$\left({t}^{\mathrm{2}} −\mathrm{3}{t}−\mathrm{1}\right)\left({t}^{\mathrm{2}} +\mathrm{2}{t}−\mathrm{1}\right)=\mathrm{0} \\ $$$${t}=−\mathrm{1}\pm\sqrt{\mathrm{2}}\vee{t}=\frac{\mathrm{3}\pm\sqrt{\mathrm{13}}}{\mathrm{2}} \\ $$$$\Rightarrow \\ $$$$\theta=\mathrm{2}{n}\pi+\frac{\pi}{\mathrm{4}}\vee\theta=\mathrm{2}{n}\pi−\frac{\mathrm{3}\pi}{\mathrm{4}}\vee\theta=\mathrm{2}{n}\pi+\mathrm{2arctan}\:\frac{\mathrm{3}\pm\sqrt{\mathrm{13}}}{\mathrm{2}} \\ $$
