Question Number 122551 by shaker last updated on 18/Nov/20

Answered by bramlexs22 last updated on 18/Nov/20
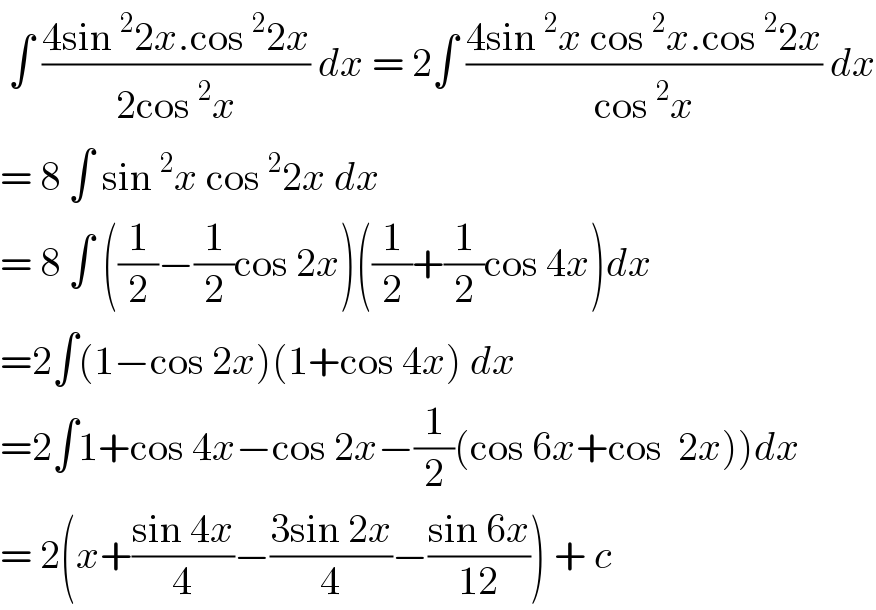
$$\:\int\:\frac{\mathrm{4sin}\:^{\mathrm{2}} \mathrm{2}{x}.\mathrm{cos}\:^{\mathrm{2}} \mathrm{2}{x}}{\mathrm{2cos}\:^{\mathrm{2}} {x}}\:{dx}\:=\:\mathrm{2}\int\:\frac{\mathrm{4sin}\:^{\mathrm{2}} {x}\:\mathrm{cos}\:^{\mathrm{2}} {x}.\mathrm{cos}\:^{\mathrm{2}} \mathrm{2}{x}}{\mathrm{cos}\:^{\mathrm{2}} {x}}\:{dx} \\ $$$$=\:\mathrm{8}\:\int\:\mathrm{sin}\:^{\mathrm{2}} {x}\:\mathrm{cos}\:^{\mathrm{2}} \mathrm{2}{x}\:{dx} \\ $$$$=\:\mathrm{8}\:\int\:\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\mathrm{2}{x}\right)\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\mathrm{4}{x}\right){dx} \\ $$$$=\mathrm{2}\int\left(\mathrm{1}−\mathrm{cos}\:\mathrm{2}{x}\right)\left(\mathrm{1}+\mathrm{cos}\:\mathrm{4}{x}\right)\:{dx}\: \\ $$$$\left.=\mathrm{2}\int\mathrm{1}+\mathrm{cos}\:\mathrm{4}{x}−\mathrm{cos}\:\mathrm{2}{x}−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{cos}\:\mathrm{6}{x}+\mathrm{cos}\:\:\mathrm{2}{x}\right)\right){dx} \\ $$$$=\:\mathrm{2}\left({x}+\frac{\mathrm{sin}\:\mathrm{4}{x}}{\mathrm{4}}−\frac{\mathrm{3sin}\:\mathrm{2}{x}}{\mathrm{4}}−\frac{\mathrm{sin}\:\mathrm{6}{x}}{\mathrm{12}}\right)\:+\:{c}\: \\ $$
Commented by MJS_new last updated on 18/Nov/20
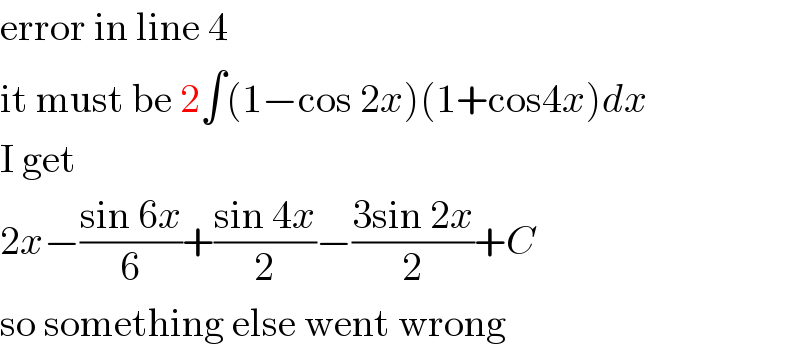
$$\mathrm{error}\:\mathrm{in}\:\mathrm{line}\:\mathrm{4} \\ $$$$\mathrm{it}\:\mathrm{must}\:\mathrm{be}\:\mathrm{2}\int\left(\mathrm{1}−\mathrm{cos}\:\mathrm{2}{x}\right)\left(\mathrm{1}+\mathrm{cos4}{x}\right){dx} \\ $$$$\mathrm{I}\:\mathrm{get} \\ $$$$\mathrm{2}{x}−\frac{\mathrm{sin}\:\mathrm{6}{x}}{\mathrm{6}}+\frac{\mathrm{sin}\:\mathrm{4}{x}}{\mathrm{2}}−\frac{\mathrm{3sin}\:\mathrm{2}{x}}{\mathrm{2}}+{C} \\ $$$$\mathrm{so}\:\mathrm{something}\:\mathrm{else}\:\mathrm{went}\:\mathrm{wrong} \\ $$
Commented by bramlexs22 last updated on 18/Nov/20
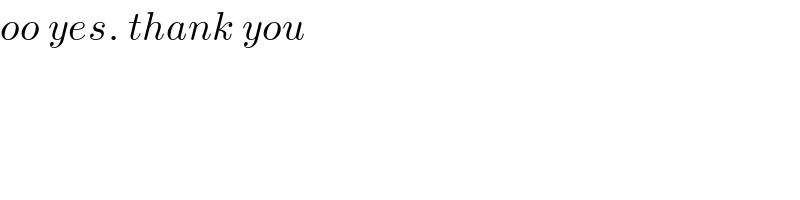
$${oo}\:{yes}.\:{thank}\:{you} \\ $$
