Menu Close

Question-122614

Tinku Tara 0 Comments
Pin




Question Number 122614 by john santu last updated on 18/Nov/20
Answered by liberty last updated on 18/Nov/20
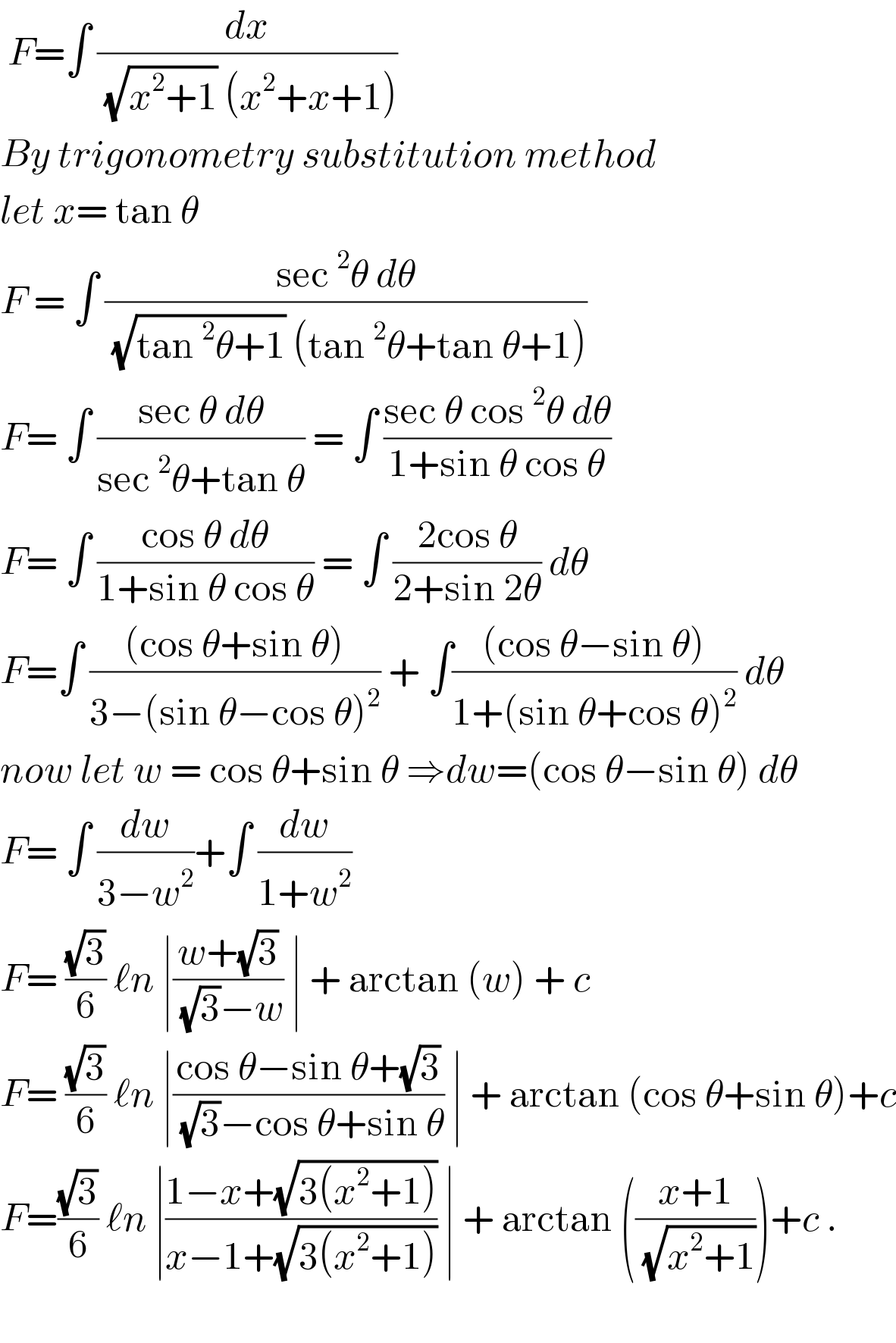
F=∫ (dx/( (√(x^2 +1)) (x^2 +x+1))) By trigonometry substitution method let x= tan θ F = ∫ ((sec^2 θ dθ)/( (√(tan^2 θ+1)) (tan^2 θ+tan θ+1))) F= ∫ ((sec θ dθ)/(sec^2 θ+tan θ)) = ∫ ((sec θ cos^2 θ dθ)/(1+sin θ cos θ)) F= ∫ ((cos θ dθ)/(1+sin θ cos θ)) = ∫ ((2cos θ)/(2+sin 2θ)) dθ F=∫ (((cos θ+sin θ))/(3−(sin θ−cos θ)^2 )) + ∫(((cos θ−sin θ))/(1+(sin θ+cos θ)^2 )) dθ now let w = cos θ+sin θ ⇒dw=(cos θ−sin θ) dθ F= ∫ (dw/(3−w^2 ))+∫ (dw/(1+w^2 )) F= ((√3)/6) ℓn ∣((w+(√3))/( (√3)−w)) ∣ + arctan (w) + c F= ((√3)/6) ℓn ∣((cos θ−sin θ+(√3))/( (√3)−cos θ+sin θ)) ∣ + arctan (cos θ+sin θ)+c F=((√3)/6) ℓn ∣((1−x+(√(3(x^2 +1))))/(x−1+(√(3(x^2 +1))))) ∣ + arctan (((x+1)/( (√(x^2 +1)))))+c .
$$\:{F}=\int\:\frac{{dx}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\:\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)} \\ $$$${By}\:{trigonometry}\:{substitution}\:{method} \\ $$$${let}\:{x}=\:\mathrm{tan}\:\theta\: \\ $$$${F}\:=\:\int\:\frac{\mathrm{sec}\:^{\mathrm{2}} \theta\:{d}\theta}{\:\sqrt{\mathrm{tan}\:^{\mathrm{2}} \theta+\mathrm{1}}\:\left(\mathrm{tan}\:^{\mathrm{2}} \theta+\mathrm{tan}\:\theta+\mathrm{1}\right)} \\ $$$${F}=\:\int\:\frac{\mathrm{sec}\:\theta\:{d}\theta}{\mathrm{sec}\:^{\mathrm{2}} \theta+\mathrm{tan}\:\theta}\:=\:\int\:\frac{\mathrm{sec}\:\theta\:\mathrm{cos}\:^{\mathrm{2}} \theta\:{d}\theta}{\mathrm{1}+\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta} \\ $$$${F}=\:\int\:\frac{\mathrm{cos}\:\theta\:{d}\theta}{\mathrm{1}+\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta}\:=\:\int\:\frac{\mathrm{2cos}\:\theta}{\mathrm{2}+\mathrm{sin}\:\mathrm{2}\theta}\:{d}\theta \\ $$$${F}=\int\:\frac{\left(\mathrm{cos}\:\theta+\mathrm{sin}\:\theta\right)}{\mathrm{3}−\left(\mathrm{sin}\:\theta−\mathrm{cos}\:\theta\right)^{\mathrm{2}} }\:+\:\int\frac{\left(\mathrm{cos}\:\theta−\mathrm{sin}\:\theta\right)}{\mathrm{1}+\left(\mathrm{sin}\:\theta+\mathrm{cos}\:\theta\right)^{\mathrm{2}} }\:{d}\theta \\ $$$${now}\:{let}\:{w}\:=\:\mathrm{cos}\:\theta+\mathrm{sin}\:\theta\:\Rightarrow{dw}=\left(\mathrm{cos}\:\theta−\mathrm{sin}\:\theta\right)\:{d}\theta \\ $$$${F}=\:\int\:\frac{{dw}}{\mathrm{3}−{w}^{\mathrm{2}} }+\int\:\frac{{dw}}{\mathrm{1}+{w}^{\mathrm{2}} }\: \\ $$$${F}=\:\frac{\sqrt{\mathrm{3}}}{\mathrm{6}}\:\ell{n}\:\mid\frac{{w}+\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{3}}−{w}}\:\mid\:+\:\mathrm{arctan}\:\left({w}\right)\:+\:{c} \\ $$$${F}=\:\frac{\sqrt{\mathrm{3}}}{\mathrm{6}}\:\ell{n}\:\mid\frac{\mathrm{cos}\:\theta−\mathrm{sin}\:\theta+\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{3}}−\mathrm{cos}\:\theta+\mathrm{sin}\:\theta}\:\mid\:+\:\mathrm{arctan}\:\left(\mathrm{cos}\:\theta+\mathrm{sin}\:\theta\right)+{c} \\ $$$${F}=\frac{\sqrt{\mathrm{3}}}{\mathrm{6}}\:\ell{n}\:\mid\frac{\mathrm{1}−{x}+\sqrt{\mathrm{3}\left({x}^{\mathrm{2}} +\mathrm{1}\right)}}{{x}−\mathrm{1}+\sqrt{\mathrm{3}\left({x}^{\mathrm{2}} +\mathrm{1}\right)}}\:\mid\:+\:\mathrm{arctan}\:\left(\frac{{x}+\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}\right)+{c}\:. \\ $$$$ \\ $$
Commented by john santu last updated on 18/Nov/20
thank you all master
$${thank}\:{you}\:{all}\:{master} \\ $$
Commented by MJS_new last updated on 18/Nov/20
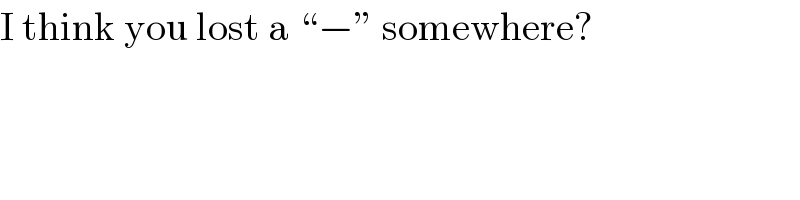
I think you lost a “−” somewhere?
$$\mathrm{I}\:\mathrm{think}\:\mathrm{you}\:\mathrm{lost}\:\mathrm{a}\:“−''\:\mathrm{somewhere}? \\ $$
Commented by liberty last updated on 18/Nov/20
in what part sir?
Commented by MJS_new last updated on 18/Nov/20
not sure. but (d/dx)[F]=−(1/( (√(x^2 +1))(x^2 +x+1))) if I am right
$$\mathrm{not}\:\mathrm{sure}.\:\mathrm{but}\:\frac{{d}}{{dx}}\left[\mathrm{F}\right]=−\frac{\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)} \\ $$$$\mathrm{if}\:\mathrm{I}\:\mathrm{am}\:\mathrm{right} \\ $$
Answered by Olaf last updated on 18/Nov/20
x = sinhu I = ∫((coshudu)/( (√(sinh^2 u+1))(sinh^2 u+sinhu+1))) I = ∫(du/( sinh^2 u+sinhu+1)) I = ∫(du/( ((e^(2u) −2+e^(−2u) )/4)+((e^u −e^(−u) )/2)+1)) I = ∫((4du)/( e^(2u) −2+e^(−2u) +2e^u −2e^(−u) +4)) I = ∫((4du)/( e^(2u) +2e^u +2−2e^(−u) +e^(−2u) )) I = ∫((4e^(2u) du)/( e^(4u) +2e^(3u) +2e^(2u) −2e^u +1)) Let ϕ = e^u I = ∫((4ϕ^2 (dϕ/ϕ))/( ϕ^4 +2ϕ^3 +2ϕ^2 −2ϕ+1)) I = ∫((4ϕdϕ)/( ϕ^4 +2ϕ^3 +2ϕ^2 −2ϕ+1)) ...4 complex roots...
$${x}\:=\:\mathrm{sinh}{u} \\ $$$$\mathrm{I}\:=\:\int\frac{\mathrm{cosh}{udu}}{\:\sqrt{\mathrm{sinh}^{\mathrm{2}} {u}+\mathrm{1}}\left(\mathrm{sinh}^{\mathrm{2}} {u}+\mathrm{sinh}{u}+\mathrm{1}\right)} \\ $$$$\mathrm{I}\:=\:\int\frac{{du}}{\:\mathrm{sinh}^{\mathrm{2}} {u}+\mathrm{sinh}{u}+\mathrm{1}} \\ $$$$\mathrm{I}\:=\:\int\frac{{du}}{\:\frac{{e}^{\mathrm{2}{u}} −\mathrm{2}+{e}^{−\mathrm{2}{u}} }{\mathrm{4}}+\frac{{e}^{{u}} −{e}^{−{u}} }{\mathrm{2}}+\mathrm{1}} \\ $$$$\mathrm{I}\:=\:\int\frac{\mathrm{4}{du}}{\:{e}^{\mathrm{2}{u}} −\mathrm{2}+{e}^{−\mathrm{2}{u}} +\mathrm{2}{e}^{{u}} −\mathrm{2}{e}^{−{u}} +\mathrm{4}} \\ $$$$\mathrm{I}\:=\:\int\frac{\mathrm{4}{du}}{\:{e}^{\mathrm{2}{u}} +\mathrm{2}{e}^{{u}} +\mathrm{2}−\mathrm{2}{e}^{−{u}} +{e}^{−\mathrm{2}{u}} } \\ $$$$\mathrm{I}\:=\:\int\frac{\mathrm{4}{e}^{\mathrm{2}{u}} {du}}{\:{e}^{\mathrm{4}{u}} +\mathrm{2}{e}^{\mathrm{3}{u}} +\mathrm{2}{e}^{\mathrm{2}{u}} −\mathrm{2}{e}^{{u}} +\mathrm{1}} \\ $$$$\mathrm{Let}\:\varphi\:=\:{e}^{{u}} \\ $$$$\mathrm{I}\:=\:\int\frac{\mathrm{4}\varphi^{\mathrm{2}} \frac{{d}\varphi}{\varphi}}{\:\varphi^{\mathrm{4}} +\mathrm{2}\varphi^{\mathrm{3}} +\mathrm{2}\varphi^{\mathrm{2}} −\mathrm{2}\varphi+\mathrm{1}} \\ $$$$\mathrm{I}\:=\:\int\frac{\mathrm{4}\varphi{d}\varphi}{\:\varphi^{\mathrm{4}} +\mathrm{2}\varphi^{\mathrm{3}} +\mathrm{2}\varphi^{\mathrm{2}} −\mathrm{2}\varphi+\mathrm{1}} \\ $$$$…\mathrm{4}\:\mathrm{complex}\:\mathrm{roots}… \\ $$
Answered by MJS_new last updated on 18/Nov/20
∫(dx/((x^2 +x+1)(√(x^2 +1))))= [t=x+(√(x^2 +1)) → dx=((√(x^2 +1))/(x+(√(x^2 +1))))dt] =4∫(t/(t^4 +2t^3 +2t^2 −2t+1))dt= =4∫(t/((t^2 +(1−(√3))t+2−(√3))(t^2 +(1+(√3))t+2+(√3))))dt= =((√3)/(12))∫(((t+2−(√3))/(t^2 +(1−(√3))t+2−(√3)))−((t+2+(√3))/(t^2 +(1+(√3))t+2+(√3))))dt= =((√3)/(24))ln ((t^2 +(1−(√3))t+2−(√3))/(t^2 +(1+(√3))t+2+(√3))) +(1/4)(arctan ((1+(√3))t−1) +arctan ((1−(√3))t−1) ...
$$\int\frac{{dx}}{\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}= \\ $$$$\:\:\:\:\:\left[{t}={x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\:\rightarrow\:{dx}=\frac{\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}{{x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}{dt}\right] \\ $$$$=\mathrm{4}\int\frac{{t}}{{t}^{\mathrm{4}} +\mathrm{2}{t}^{\mathrm{3}} +\mathrm{2}{t}^{\mathrm{2}} −\mathrm{2}{t}+\mathrm{1}}{dt}= \\ $$$$=\mathrm{4}\int\frac{{t}}{\left({t}^{\mathrm{2}} +\left(\mathrm{1}−\sqrt{\mathrm{3}}\right){t}+\mathrm{2}−\sqrt{\mathrm{3}}\right)\left({t}^{\mathrm{2}} +\left(\mathrm{1}+\sqrt{\mathrm{3}}\right){t}+\mathrm{2}+\sqrt{\mathrm{3}}\right)}{dt}= \\ $$$$=\frac{\sqrt{\mathrm{3}}}{\mathrm{12}}\int\left(\frac{{t}+\mathrm{2}−\sqrt{\mathrm{3}}}{{t}^{\mathrm{2}} +\left(\mathrm{1}−\sqrt{\mathrm{3}}\right){t}+\mathrm{2}−\sqrt{\mathrm{3}}}−\frac{{t}+\mathrm{2}+\sqrt{\mathrm{3}}}{{t}^{\mathrm{2}} +\left(\mathrm{1}+\sqrt{\mathrm{3}}\right){t}+\mathrm{2}+\sqrt{\mathrm{3}}}\right){dt}= \\ $$$$=\frac{\sqrt{\mathrm{3}}}{\mathrm{24}}\mathrm{ln}\:\frac{{t}^{\mathrm{2}} +\left(\mathrm{1}−\sqrt{\mathrm{3}}\right){t}+\mathrm{2}−\sqrt{\mathrm{3}}}{{t}^{\mathrm{2}} +\left(\mathrm{1}+\sqrt{\mathrm{3}}\right){t}+\mathrm{2}+\sqrt{\mathrm{3}}}\:+\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{arctan}\:\left(\left(\mathrm{1}+\sqrt{\mathrm{3}}\right){t}−\mathrm{1}\right)\:+\mathrm{arctan}\:\left(\left(\mathrm{1}−\sqrt{\mathrm{3}}\right){t}−\mathrm{1}\right)\right. \\ $$$$… \\ $$
Answered by mathmax by abdo last updated on 18/Nov/20
A =∫ (dx/( (√(1+x^2 ))(x^2 +x+1))) we do the changement x=sht ⇒ A =∫ ((cht)/(cht(sh^2 t+sht +1)))dt =∫ (dt/(((ch(2t)−1)/2)+sh(t)+1)) =∫ ((2dt)/(ch(2t)−1+2sh(t)+2)) =∫ ((2dt)/(((e^(2t) +e^(−2t) )/2)+e^t −e^(−t) +1)) =∫ ((4dt)/(e^(2t) +e^(−2t) +2e^t −2e^(−t) +2)) =_(e^t =u) ∫ ((4du)/(u(u^2 +u^(−2) +2u−2u^(−1) +2))) =∫ ((4du)/(u^(3 ) +u^(−1) +2u^2 −2+2u)) =∫ ((4u du)/(u^4 +1+2u^3 −2u +2u^2 )) =∫ ((4udu)/(u^4 +2u^3 +2u^2 −2u +1)) rest decomposition of f(u) =((4u)/(u^4 +2u^3 +2u^2 −2u +1)) ...be continued....
$$\mathrm{A}\:=\int\:\:\frac{\mathrm{dx}}{\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{1}\right)}\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\mathrm{x}=\mathrm{sht}\:\Rightarrow \\ $$$$\mathrm{A}\:=\int\:\:\:\frac{\mathrm{cht}}{\mathrm{cht}\left(\mathrm{sh}^{\mathrm{2}} \mathrm{t}+\mathrm{sht}\:+\mathrm{1}\right)}\mathrm{dt}\:=\int\:\:\frac{\mathrm{dt}}{\frac{\mathrm{ch}\left(\mathrm{2t}\right)−\mathrm{1}}{\mathrm{2}}+\mathrm{sh}\left(\mathrm{t}\right)+\mathrm{1}} \\ $$$$=\int\:\:\frac{\mathrm{2dt}}{\mathrm{ch}\left(\mathrm{2t}\right)−\mathrm{1}+\mathrm{2sh}\left(\mathrm{t}\right)+\mathrm{2}}\:=\int\:\:\frac{\mathrm{2dt}}{\frac{\mathrm{e}^{\mathrm{2t}} +\mathrm{e}^{−\mathrm{2t}} }{\mathrm{2}}+\mathrm{e}^{\mathrm{t}} −\mathrm{e}^{−\mathrm{t}} +\mathrm{1}} \\ $$$$=\int\:\frac{\mathrm{4dt}}{\mathrm{e}^{\mathrm{2t}} \:+\mathrm{e}^{−\mathrm{2t}} \:+\mathrm{2e}^{\mathrm{t}} −\mathrm{2e}^{−\mathrm{t}} \:+\mathrm{2}}\:=_{\mathrm{e}^{\mathrm{t}} \:=\mathrm{u}} \:\:\:\:\int\:\:\:\frac{\mathrm{4du}}{\mathrm{u}\left(\mathrm{u}^{\mathrm{2}} \:+\mathrm{u}^{−\mathrm{2}} \:+\mathrm{2u}−\mathrm{2u}^{−\mathrm{1}} \:+\mathrm{2}\right)} \\ $$$$=\int\:\:\frac{\mathrm{4du}}{\mathrm{u}^{\mathrm{3}\:} \:+\mathrm{u}^{−\mathrm{1}} \:+\mathrm{2u}^{\mathrm{2}} −\mathrm{2}+\mathrm{2u}}\:=\int\:\:\frac{\mathrm{4u}\:\mathrm{du}}{\mathrm{u}^{\mathrm{4}} \:+\mathrm{1}+\mathrm{2u}^{\mathrm{3}} −\mathrm{2u}\:+\mathrm{2u}^{\mathrm{2}} } \\ $$$$=\int\:\:\frac{\mathrm{4udu}}{\mathrm{u}^{\mathrm{4}} \:+\mathrm{2u}^{\mathrm{3}} +\mathrm{2u}^{\mathrm{2}} \:−\mathrm{2u}\:+\mathrm{1}}\:\:\mathrm{rest}\:\mathrm{decomposition}\:\mathrm{of} \\ $$$$\mathrm{f}\left(\mathrm{u}\right)\:=\frac{\mathrm{4u}}{\mathrm{u}^{\mathrm{4}} \:+\mathrm{2u}^{\mathrm{3}} \:+\mathrm{2u}^{\mathrm{2}} −\mathrm{2u}\:+\mathrm{1}}\:…\mathrm{be}\:\mathrm{continued}…. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *