Question Number 122626 by rs4089 last updated on 18/Nov/20
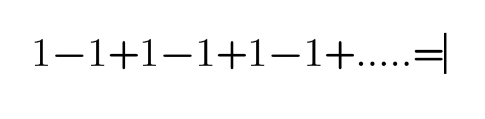
Answered by Dwaipayan Shikari last updated on 18/Nov/20
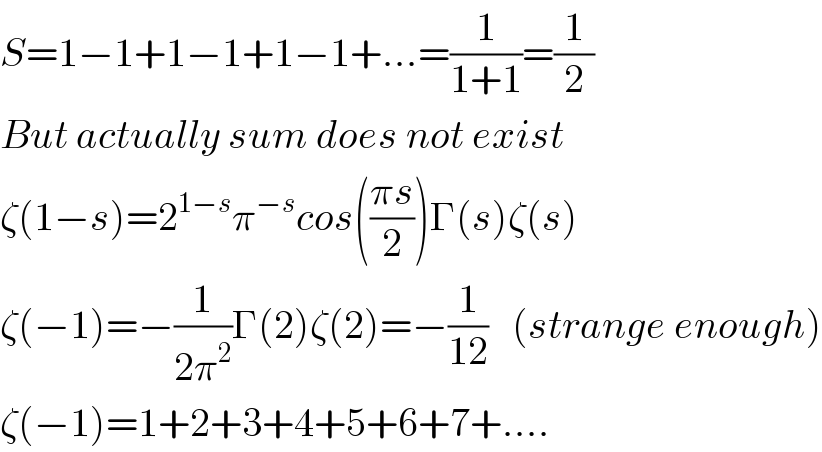
$${S}=\mathrm{1}−\mathrm{1}+\mathrm{1}−\mathrm{1}+\mathrm{1}−\mathrm{1}+…=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${But}\:{actually}\:{sum}\:{does}\:{not}\:{exist} \\ $$$$\zeta\left(\mathrm{1}−{s}\right)=\mathrm{2}^{\mathrm{1}−{s}} \pi^{−{s}} {cos}\left(\frac{\pi{s}}{\mathrm{2}}\right)\Gamma\left({s}\right)\zeta\left({s}\right) \\ $$$$\zeta\left(−\mathrm{1}\right)=−\frac{\mathrm{1}}{\mathrm{2}\pi^{\mathrm{2}} }\Gamma\left(\mathrm{2}\right)\zeta\left(\mathrm{2}\right)=−\frac{\mathrm{1}}{\mathrm{12}}\:\:\:\left({strange}\:{enough}\right) \\ $$$$\zeta\left(−\mathrm{1}\right)=\mathrm{1}+\mathrm{2}+\mathrm{3}+\mathrm{4}+\mathrm{5}+\mathrm{6}+\mathrm{7}+…. \\ $$
Answered by mathmax by abdo last updated on 18/Nov/20
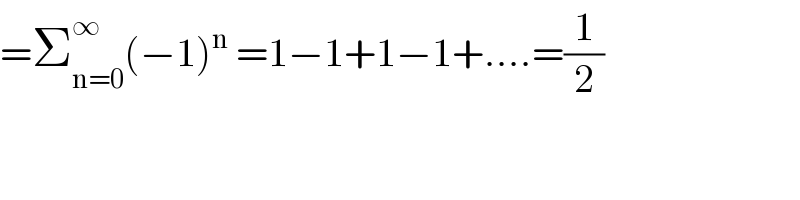
$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \:=\mathrm{1}−\mathrm{1}+\mathrm{1}−\mathrm{1}+….=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
