Question-122715

Question Number 122715 by ZiYangLee last updated on 19/Nov/20

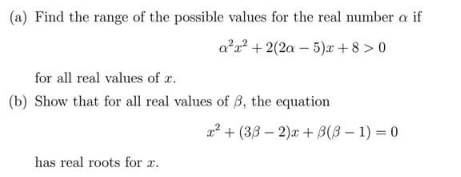
Answered by liberty last updated on 19/Nov/20

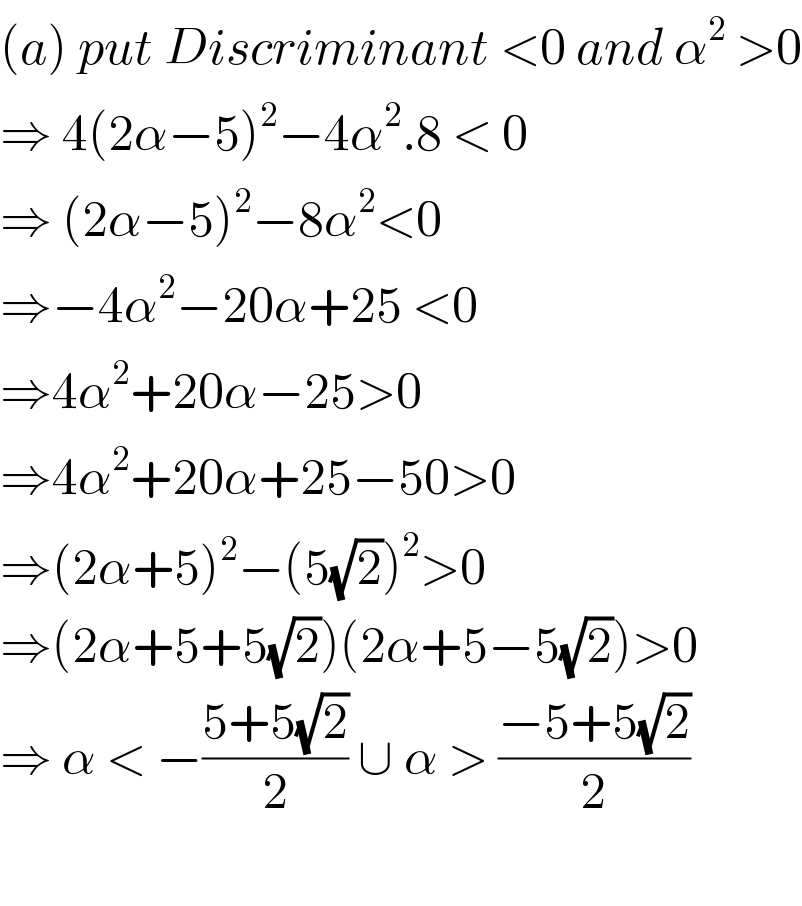
(a) put Discriminant <0 and α^2 >0 ⇒ 4(2α−5)^2 −4α^2 .8 < 0 ⇒ (2α−5)^2 −8α^2 <0 ⇒−4α^2 −20α+25 <0 ⇒4α^2 +20α−25>0 ⇒4α^2 +20α+25−50>0 ⇒(2α+5)^2 −(5(√2))^2 >0 ⇒(2α+5+5(√2))(2α+5−5(√2))>0 ⇒ α < −((5+5(√2))/2) ∪ α > ((−5+5(√2))/2)

$$\left({a}\right)\:{put}\:{Discriminant}\:<\mathrm{0}\:{and}\:\alpha^{\mathrm{2}} \:>\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{4}\left(\mathrm{2}\alpha−\mathrm{5}\right)^{\mathrm{2}} −\mathrm{4}\alpha^{\mathrm{2}} .\mathrm{8}\:<\:\mathrm{0} \\ $$$$\Rightarrow\:\left(\mathrm{2}\alpha−\mathrm{5}\right)^{\mathrm{2}} −\mathrm{8}\alpha^{\mathrm{2}} <\mathrm{0} \\ $$$$\Rightarrow−\mathrm{4}\alpha^{\mathrm{2}} −\mathrm{20}\alpha+\mathrm{25}\:<\mathrm{0} \\ $$$$\Rightarrow\mathrm{4}\alpha^{\mathrm{2}} +\mathrm{20}\alpha−\mathrm{25}>\mathrm{0} \\ $$$$\Rightarrow\mathrm{4}\alpha^{\mathrm{2}} +\mathrm{20}\alpha+\mathrm{25}−\mathrm{50}>\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{2}\alpha+\mathrm{5}\right)^{\mathrm{2}} −\left(\mathrm{5}\sqrt{\mathrm{2}}\right)^{\mathrm{2}} >\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{2}\alpha+\mathrm{5}+\mathrm{5}\sqrt{\mathrm{2}}\right)\left(\mathrm{2}\alpha+\mathrm{5}−\mathrm{5}\sqrt{\mathrm{2}}\right)>\mathrm{0} \\ $$$$\Rightarrow\:\alpha\:<\:−\frac{\mathrm{5}+\mathrm{5}\sqrt{\mathrm{2}}}{\mathrm{2}}\:\cup\:\alpha\:>\:\frac{−\mathrm{5}+\mathrm{5}\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$$ \\ $$

Facebook Tweet Pin

Question-122715

Leave a Reply Cancel reply