Question Number 122734 by bemath last updated on 19/Nov/20
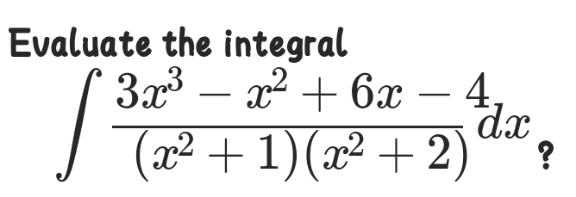
Answered by liberty last updated on 19/Nov/20

$$\:{Just}\:{applying}\:{partial}\:{faction} \\ $$$$\:\frac{\mathrm{3}{x}^{\mathrm{3}} −{x}^{\mathrm{2}} +\mathrm{6}{x}−\mathrm{4}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{2}\right)}\:=\:\frac{{Ax}+{B}}{{x}^{\mathrm{2}} +\mathrm{1}}+\:\frac{{Cx}+{D}}{{x}^{\mathrm{2}} +\mathrm{2}} \\ $$$$\:{gives}\:{A}=\mathrm{3}\:,\:{B}=−\mathrm{3}\:,\:{C}=\mathrm{0}\:{and}\:{D}=\mathrm{2} \\ $$$${W}\left({x}\right)=\int\:\frac{\mathrm{3}{x}−\mathrm{3}}{{x}^{\mathrm{2}} +\mathrm{1}}\:+\:\frac{\mathrm{2}}{{x}^{\mathrm{2}} +\mathrm{2}}\:{dx}\: \\ $$$${W}\left({x}\right)=\:\frac{\mathrm{3}}{\mathrm{2}}\int\:\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\mathrm{1}}{dx}−\int\frac{\mathrm{3}}{{x}^{\mathrm{2}} +\mathrm{1}}{dx}+\int\frac{\mathrm{2}}{{x}^{\mathrm{2}} +\mathrm{2}}{dx} \\ $$$${W}\left({x}\right)=\frac{\mathrm{3}\ell{n}\left({x}^{\mathrm{2}} +\mathrm{1}\right)}{\mathrm{2}}−\mathrm{3}\:\mathrm{tan}^{−\mathrm{1}} \left({x}\right)+\sqrt{\mathrm{2}}\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{{x}}{\:\sqrt{\mathrm{2}}}\right)+\:{c} \\ $$
