Question Number 122773 by solstis last updated on 19/Nov/20

Answered by MJS_new last updated on 19/Nov/20
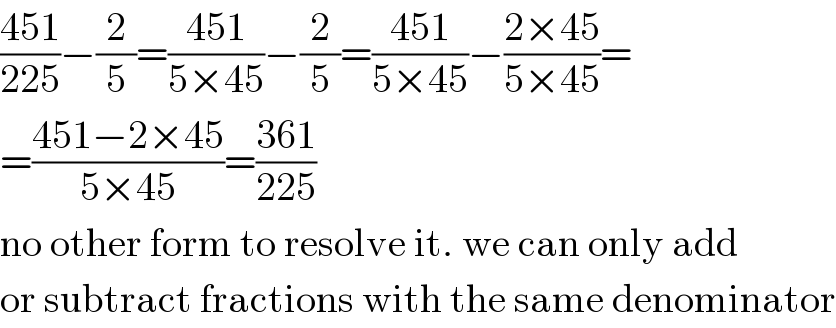
$$\frac{\mathrm{451}}{\mathrm{225}}−\frac{\mathrm{2}}{\mathrm{5}}=\frac{\mathrm{451}}{\mathrm{5}×\mathrm{45}}−\frac{\mathrm{2}}{\mathrm{5}}=\frac{\mathrm{451}}{\mathrm{5}×\mathrm{45}}−\frac{\mathrm{2}×\mathrm{45}}{\mathrm{5}×\mathrm{45}}= \\ $$$$=\frac{\mathrm{451}−\mathrm{2}×\mathrm{45}}{\mathrm{5}×\mathrm{45}}=\frac{\mathrm{361}}{\mathrm{225}} \\ $$$$\mathrm{no}\:\mathrm{other}\:\mathrm{form}\:\mathrm{to}\:\mathrm{resolve}\:\mathrm{it}.\:\mathrm{we}\:\mathrm{can}\:\mathrm{only}\:\mathrm{add} \\ $$$$\mathrm{or}\:\mathrm{subtract}\:\mathrm{fractions}\:\mathrm{with}\:\mathrm{the}\:\mathrm{same}\:\mathrm{denominator} \\ $$
Commented by solstis last updated on 19/Nov/20
$$\mathrm{one}\:\mathrm{million}\:\mathrm{thank}!! \\ $$
Commented by MJS_new last updated on 19/Nov/20
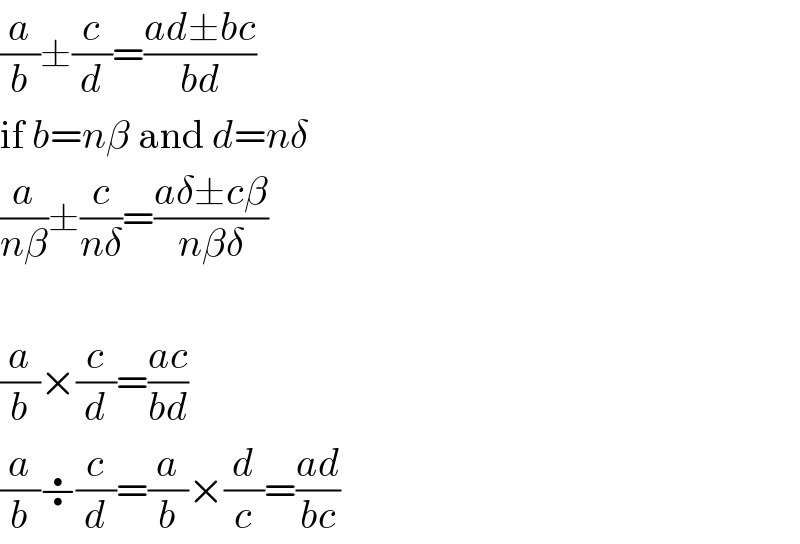
$$\frac{{a}}{{b}}\pm\frac{{c}}{{d}}=\frac{{ad}\pm{bc}}{{bd}} \\ $$$$\mathrm{if}\:{b}={n}\beta\:\mathrm{and}\:{d}={n}\delta \\ $$$$\frac{{a}}{{n}\beta}\pm\frac{{c}}{{n}\delta}=\frac{{a}\delta\pm{c}\beta}{{n}\beta\delta} \\ $$$$ \\ $$$$\frac{{a}}{{b}}×\frac{{c}}{{d}}=\frac{{ac}}{{bd}} \\ $$$$\frac{{a}}{{b}}\boldsymbol{\div}\frac{{c}}{{d}}=\frac{{a}}{{b}}×\frac{{d}}{{c}}=\frac{{ad}}{{bc}} \\ $$
