Question Number 122776 by shaker last updated on 19/Nov/20
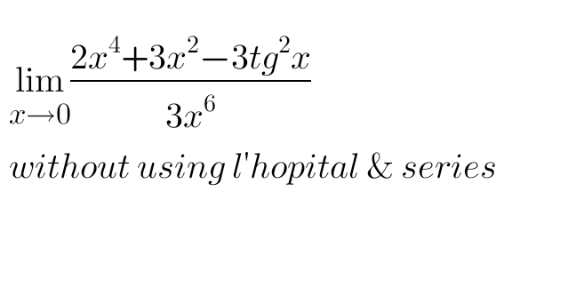
Answered by mathmax by abdo last updated on 19/Nov/20

$$\mathrm{without}\:\mathrm{using}\:\mathrm{anything}….! \\ $$
Answered by kaivan.ahmadi last updated on 19/Nov/20
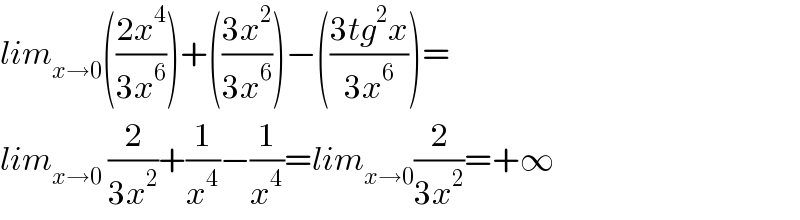
$${lim}_{{x}\rightarrow\mathrm{0}} \left(\frac{\mathrm{2}{x}^{\mathrm{4}} }{\mathrm{3}{x}^{\mathrm{6}} }\right)+\left(\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{3}{x}^{\mathrm{6}} }\right)−\left(\frac{\mathrm{3}{tg}^{\mathrm{2}} {x}}{\mathrm{3}{x}^{\mathrm{6}} }\right)= \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} \:\frac{\mathrm{2}}{\mathrm{3}{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{{x}^{\mathrm{4}} }−\frac{\mathrm{1}}{{x}^{\mathrm{4}} }={lim}_{{x}\rightarrow\mathrm{0}} \frac{\mathrm{2}}{\mathrm{3}{x}^{\mathrm{2}} }=+\infty \\ $$
