Question Number 122798 by aurpeyz last updated on 19/Nov/20
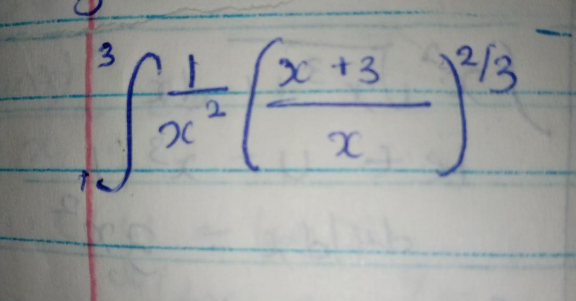
Commented by mohammad17 last updated on 19/Nov/20
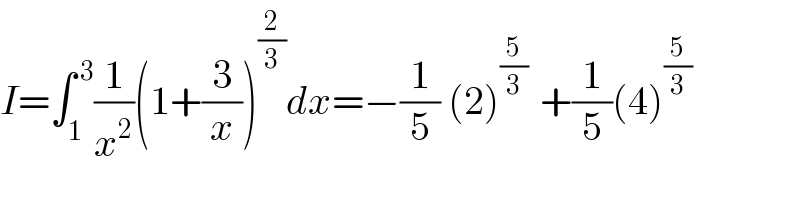
$${I}=\int_{\mathrm{1}} ^{\:\mathrm{3}} \frac{\mathrm{1}}{{x}^{\mathrm{2}} }\left(\mathrm{1}+\frac{\mathrm{3}}{{x}}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} {dx}=−\frac{\mathrm{1}}{\mathrm{5}}\:\left(\mathrm{2}\right)^{\frac{\mathrm{5}}{\mathrm{3}}\:} \:+\frac{\mathrm{1}}{\mathrm{5}}\left(\mathrm{4}\right)^{\frac{\mathrm{5}}{\mathrm{3}}} \\ $$
Answered by MJS_new last updated on 19/Nov/20
![∫(1/x^2 )(((x+3)/x))^(2/3) dx= [t=(((x+3)/x))^(1/3) → dx=−(x+3)^(2/3) x^(4/3) dt] =−∫t^4 dt=−(t^5 /5)=−(((x+3)^(5/3) )/(5x^(5/3) ))+C ⇏ ∫_1 ^3 (1/x^2 )(((x+3)/x))^(2/3) dx=((2(2)^(1/3) )/5)(4−(2)^(1/3) )](https://www.tinkutara.com/question/Q122817.png)
$$\int\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\left(\frac{{x}+\mathrm{3}}{{x}}\right)^{\mathrm{2}/\mathrm{3}} {dx}= \\ $$$$\:\:\:\:\:\left[{t}=\left(\frac{{x}+\mathrm{3}}{{x}}\right)^{\mathrm{1}/\mathrm{3}} \:\rightarrow\:{dx}=−\left({x}+\mathrm{3}\right)^{\mathrm{2}/\mathrm{3}} {x}^{\mathrm{4}/\mathrm{3}} {dt}\right] \\ $$$$=−\int{t}^{\mathrm{4}} {dt}=−\frac{{t}^{\mathrm{5}} }{\mathrm{5}}=−\frac{\left({x}+\mathrm{3}\right)^{\mathrm{5}/\mathrm{3}} }{\mathrm{5}{x}^{\mathrm{5}/\mathrm{3}} }+{C} \\ $$$$\nRightarrow \\ $$$$\underset{\mathrm{1}} {\overset{\mathrm{3}} {\int}}\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\left(\frac{{x}+\mathrm{3}}{{x}}\right)^{\mathrm{2}/\mathrm{3}} {dx}=\frac{\mathrm{2}\sqrt[{\mathrm{3}}]{\mathrm{2}}}{\mathrm{5}}\left(\mathrm{4}−\sqrt[{\mathrm{3}}]{\mathrm{2}}\right) \\ $$
Answered by Dwaipayan Shikari last updated on 20/Nov/20
![∫_1 ^3 (1/x^2 )(((x+3)/x))^(2/3) dx =−(1/6)∫_1 ^3 −(6/x^2 )(1+(3/x))^(2/3) dx =(1/6)∫_2 ^4 t^(2/3) dt =(1/(10))[t^(5/3) ]_2 ^4 =(4/5)(2)^(1/3) −(1/5)(2^2 )^(1/3)](https://www.tinkutara.com/question/Q122846.png)
$$\int_{\mathrm{1}} ^{\mathrm{3}} \frac{\mathrm{1}}{{x}^{\mathrm{2}} }\left(\frac{{x}+\mathrm{3}}{{x}}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} {dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{6}}\int_{\mathrm{1}} ^{\mathrm{3}} −\frac{\mathrm{6}}{{x}^{\mathrm{2}} }\left(\mathrm{1}+\frac{\mathrm{3}}{{x}}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} {dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\int_{\mathrm{2}} ^{\mathrm{4}} {t}^{\frac{\mathrm{2}}{\mathrm{3}}} {dt}\:=\frac{\mathrm{1}}{\mathrm{10}}\left[{t}^{\frac{\mathrm{5}}{\mathrm{3}}} \right]_{\mathrm{2}} ^{\mathrm{4}} =\frac{\mathrm{4}}{\mathrm{5}}\sqrt[{\mathrm{3}}]{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{5}}\sqrt[{\mathrm{3}}]{\mathrm{2}^{\mathrm{2}} } \\ $$
