Question Number 122799 by aurpeyz last updated on 19/Nov/20
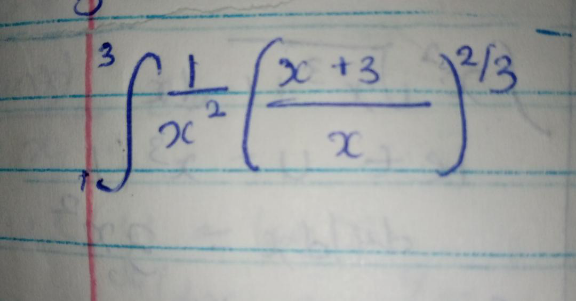
Answered by liberty last updated on 19/Nov/20
![letting u = 1+3x^(−1) ⇒du=−3x^(−2) dx L(x)=−(1/3)∫ u^(2/3) du = −(1/3)×(3/5)u^(5/3) + c thus ∫_1 ^3 x^(−2) (1+3x^(−1) )^(2/3) dx = −(1/5)[(1+3x^(−1) )^(5/3) ]_1 ^3 = −(1/5) [ 2(4)^(1/3) −4((16))^(1/3) ] = (2/5) [ 2((16))^(1/3) −(4)^(1/3) ] = (2/5) [ 4(2)^(1/3) −(4)^(1/3) ]](https://www.tinkutara.com/question/Q122819.png)
$${letting}\:{u}\:=\:\mathrm{1}+\mathrm{3}{x}^{−\mathrm{1}} \:\Rightarrow{du}=−\mathrm{3}{x}^{−\mathrm{2}} {dx} \\ $$$${L}\left({x}\right)=−\frac{\mathrm{1}}{\mathrm{3}}\int\:{u}^{\frac{\mathrm{2}}{\mathrm{3}}} \:{du}\:\:=\:−\frac{\mathrm{1}}{\mathrm{3}}×\frac{\mathrm{3}}{\mathrm{5}}{u}^{\frac{\mathrm{5}}{\mathrm{3}}} +\:{c} \\ $$$${thus}\:\underset{\mathrm{1}} {\overset{\mathrm{3}} {\int}}\:{x}^{−\mathrm{2}} \left(\mathrm{1}+\mathrm{3}{x}^{−\mathrm{1}} \right)^{\frac{\mathrm{2}}{\mathrm{3}}} {dx}\:=\:−\frac{\mathrm{1}}{\mathrm{5}}\left[\left(\mathrm{1}+\mathrm{3}{x}^{−\mathrm{1}} \right)^{\frac{\mathrm{5}}{\mathrm{3}}} \right]_{\mathrm{1}} ^{\mathrm{3}} \\ $$$$\:=\:−\frac{\mathrm{1}}{\mathrm{5}}\:\left[\:\mathrm{2}\sqrt[{\mathrm{3}}]{\mathrm{4}}\:−\mathrm{4}\sqrt[{\mathrm{3}}]{\mathrm{16}}\:\right]\:=\:\frac{\mathrm{2}}{\mathrm{5}}\:\left[\:\mathrm{2}\sqrt[{\mathrm{3}}]{\mathrm{16}}−\sqrt[{\mathrm{3}}]{\mathrm{4}}\:\right] \\ $$$$=\:\frac{\mathrm{2}}{\mathrm{5}}\:\left[\:\mathrm{4}\sqrt[{\mathrm{3}}]{\mathrm{2}}\:−\sqrt[{\mathrm{3}}]{\mathrm{4}}\:\right]\: \\ $$
