Question Number 122807 by TITA last updated on 19/Nov/20

Commented by TITA last updated on 19/Nov/20

$${please}\:{help} \\ $$
Answered by ebi last updated on 20/Nov/20
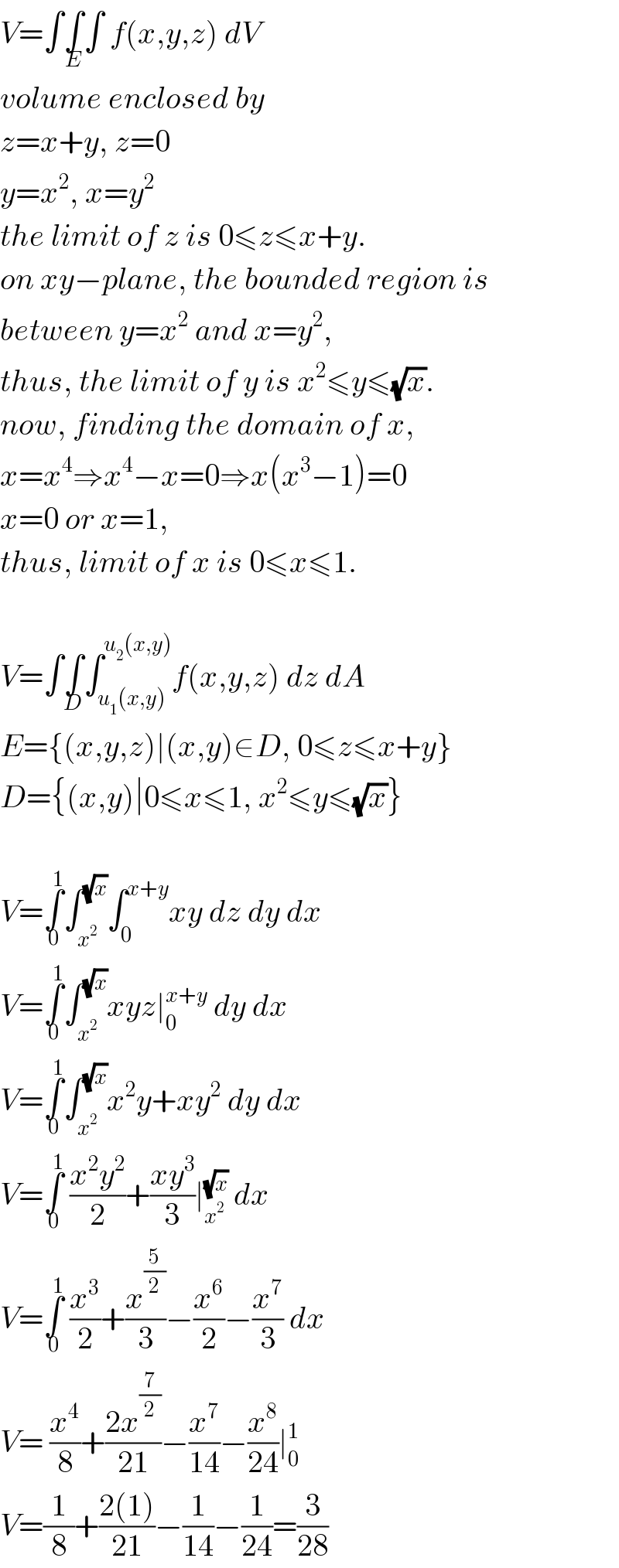
$${V}=\int\underset{{E}} {\int}\int\:{f}\left({x},{y},{z}\right)\:{dV} \\ $$$${volume}\:{enclosed}\:{by} \\ $$$${z}={x}+{y},\:{z}=\mathrm{0} \\ $$$${y}={x}^{\mathrm{2}} ,\:{x}={y}^{\mathrm{2}} \\ $$$${the}\:{limit}\:{of}\:{z}\:{is}\:\mathrm{0}\leqslant{z}\leqslant{x}+{y}. \\ $$$${on}\:{xy}−{plane},\:{the}\:{bounded}\:{region}\:{is} \\ $$$${between}\:{y}={x}^{\mathrm{2}} \:{and}\:{x}={y}^{\mathrm{2}} , \\ $$$${thus},\:{the}\:{limit}\:{of}\:{y}\:{is}\:{x}^{\mathrm{2}} \leqslant{y}\leqslant\sqrt{{x}}. \\ $$$${now},\:{finding}\:{the}\:{domain}\:{of}\:{x}, \\ $$$${x}={x}^{\mathrm{4}} \Rightarrow{x}^{\mathrm{4}} −{x}=\mathrm{0}\Rightarrow{x}\left({x}^{\mathrm{3}} −\mathrm{1}\right)=\mathrm{0} \\ $$$${x}=\mathrm{0}\:{or}\:{x}=\mathrm{1}, \\ $$$${thus},\:{limit}\:{of}\:{x}\:{is}\:\mathrm{0}\leqslant{x}\leqslant\mathrm{1}. \\ $$$$ \\ $$$${V}=\int\underset{{D}} {\int}\int_{{u}_{\mathrm{1}} \left({x},{y}\right)} ^{{u}_{\mathrm{2}} \left({x},{y}\right)} {f}\left({x},{y},{z}\right)\:{dz}\:{dA} \\ $$$${E}=\left\{\left({x},{y},{z}\right)\mid\left({x},{y}\right)\in{D},\:\mathrm{0}\leqslant{z}\leqslant{x}+{y}\right\} \\ $$$${D}=\left\{\left({x},{y}\right)\mid\mathrm{0}\leqslant{x}\leqslant\mathrm{1},\:{x}^{\mathrm{2}} \leqslant{y}\leqslant\sqrt{{x}}\right\} \\ $$$$ \\ $$$${V}=\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\int_{{x}^{\mathrm{2}} } ^{\sqrt{{x}}} \int_{\mathrm{0}} ^{{x}+{y}} {xy}\:{dz}\:{dy}\:{dx} \\ $$$${V}=\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\int_{{x}^{\mathrm{2}} } ^{\sqrt{{x}}} {xyz}\mid_{\mathrm{0}} ^{{x}+{y}} \:{dy}\:{dx} \\ $$$${V}=\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\int_{{x}^{\mathrm{2}} } ^{\sqrt{{x}}} {x}^{\mathrm{2}} {y}+{xy}^{\mathrm{2}} \:{dy}\:{dx} \\ $$$${V}=\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\frac{{x}^{\mathrm{2}} {y}^{\mathrm{2}} }{\mathrm{2}}+\frac{{xy}^{\mathrm{3}} }{\mathrm{3}}\mid_{{x}^{\mathrm{2}} } ^{\sqrt{{x}}} \:{dx} \\ $$$${V}=\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\frac{{x}^{\mathrm{3}} }{\mathrm{2}}+\frac{{x}^{\frac{\mathrm{5}}{\mathrm{2}}} }{\mathrm{3}}−\frac{{x}^{\mathrm{6}} }{\mathrm{2}}−\frac{{x}^{\mathrm{7}} }{\mathrm{3}}\:{dx} \\ $$$${V}=\:\frac{{x}^{\mathrm{4}} }{\mathrm{8}}+\frac{\mathrm{2}{x}^{\frac{\mathrm{7}}{\mathrm{2}}} }{\mathrm{21}}−\frac{{x}^{\mathrm{7}} }{\mathrm{14}}−\frac{{x}^{\mathrm{8}} }{\mathrm{24}}\mid_{\mathrm{0}} ^{\mathrm{1}} \\ $$$${V}=\frac{\mathrm{1}}{\mathrm{8}}+\frac{\mathrm{2}\left(\mathrm{1}\right)}{\mathrm{21}}−\frac{\mathrm{1}}{\mathrm{14}}−\frac{\mathrm{1}}{\mathrm{24}}=\frac{\mathrm{3}}{\mathrm{28}} \\ $$
