Question Number 122823 by bemath last updated on 19/Nov/20
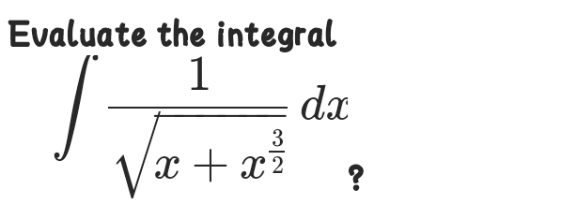
Answered by liberty last updated on 19/Nov/20

$$\:{L}\left({x}\right)\:=\:\int\:\frac{\mathrm{1}}{\:\sqrt{{x}\left(\mathrm{1}+\sqrt{{x}}\right)}}\:{dx}\:=\:\int\:\frac{\mathrm{1}}{\:\sqrt{{x}}\:\sqrt{\mathrm{1}+\sqrt{{x}}}\:}\:{dx} \\ $$$${let}\:{u}\:=\:\mathrm{1}+\sqrt{{x}}\:\Rightarrow{du}\:=\:\frac{{dx}}{\mathrm{2}\sqrt{{x}}} \\ $$$${L}\left({x}\right)\:=\:\mathrm{2}\int\:\frac{\mathrm{1}}{\:\sqrt{{u}}}\:{du}\:=\:\mathrm{4}\sqrt{{u}}\:+\:{c}\:\: \\ $$$${L}\left({x}\right)=\:\mathrm{4}\sqrt{\mathrm{1}+\sqrt{{x}}}\:+\:{c}\: \\ $$
