Question Number 122860 by greg_ed last updated on 20/Nov/20

Answered by MJS_new last updated on 20/Nov/20
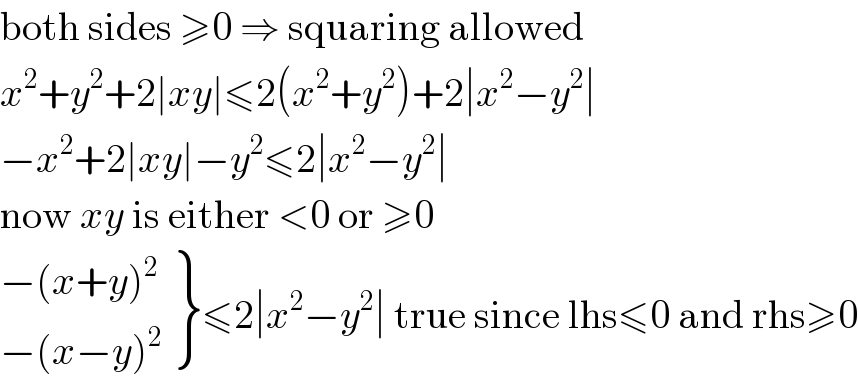
$$\mathrm{both}\:\mathrm{sides}\:\geqslant\mathrm{0}\:\Rightarrow\:\mathrm{squaring}\:\mathrm{allowed} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{2}\mid{xy}\mid\leqslant\mathrm{2}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)+\mathrm{2}\mid{x}^{\mathrm{2}} −{y}^{\mathrm{2}} \mid \\ $$$$−{x}^{\mathrm{2}} +\mathrm{2}\mid{xy}\mid−{y}^{\mathrm{2}} \leqslant\mathrm{2}\mid{x}^{\mathrm{2}} −{y}^{\mathrm{2}} \mid \\ $$$$\mathrm{now}\:{xy}\:\mathrm{is}\:\mathrm{either}\:<\mathrm{0}\:\mathrm{or}\:\geqslant\mathrm{0} \\ $$$$\left.\begin{matrix}{−\left({x}+{y}\right)^{\mathrm{2}} }\\{−\left({x}−{y}\right)^{\mathrm{2}} }\end{matrix}\right\}\leqslant\mathrm{2}\mid{x}^{\mathrm{2}} −{y}^{\mathrm{2}} \mid\:\mathrm{true}\:\mathrm{since}\:\mathrm{lhs}\leqslant\mathrm{0}\:\mathrm{and}\:\mathrm{rhs}\geqslant\mathrm{0} \\ $$
Commented by greg_ed last updated on 20/Nov/20

$$\mathrm{thanks}. \\ $$$$\mathrm{but},\:\mathrm{i}\:\mathrm{need}\:\mathrm{another}\:\mathrm{way}\:!\: \\ $$
