Question Number 122884 by CanovasCamiseros last updated on 20/Nov/20

Commented by CanovasCamiseros last updated on 20/Nov/20
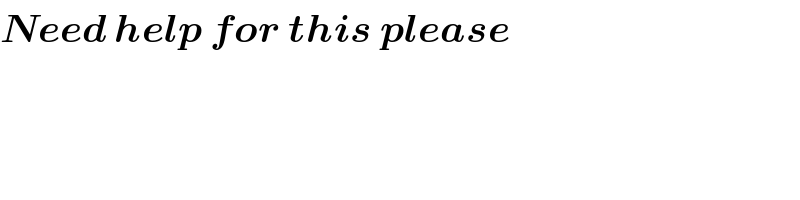
$$\boldsymbol{{Need}}\:\boldsymbol{{help}}\:\boldsymbol{{for}}\:\boldsymbol{{this}}\:\boldsymbol{{please}} \\ $$
Answered by MJS_new last updated on 20/Nov/20

$$\sqrt{\mathrm{e}^{{x}} }=\mathrm{e}^{\frac{{x}}{\mathrm{2}}} \\ $$$$\int\sqrt{\mathrm{e}^{{x}} }{dx}=\mathrm{2e}^{\frac{{x}}{\mathrm{2}}} +{C} \\ $$
Commented by MJS_new last updated on 20/Nov/20
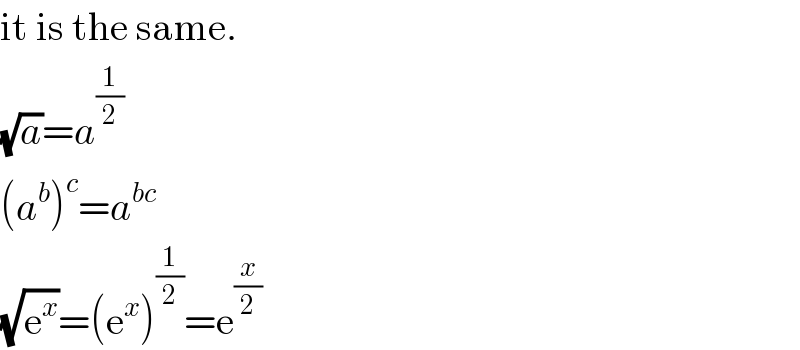
$$\mathrm{it}\:\mathrm{is}\:\mathrm{the}\:\mathrm{same}. \\ $$$$\sqrt{{a}}={a}^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\left({a}^{{b}} \right)^{{c}} ={a}^{{bc}} \\ $$$$\sqrt{\mathrm{e}^{{x}} }=\left(\mathrm{e}^{{x}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} =\mathrm{e}^{\frac{{x}}{\mathrm{2}}} \\ $$
Commented by CanovasCamiseros last updated on 20/Nov/20
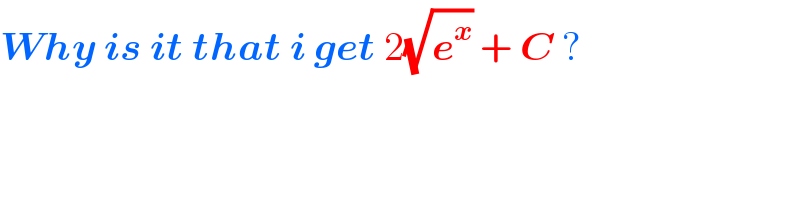
$$\boldsymbol{{Why}}\:\boldsymbol{{is}}\:\boldsymbol{{it}}\:\boldsymbol{{that}}\:\boldsymbol{{i}}\:\boldsymbol{{get}}\:\mathrm{2}\sqrt{\boldsymbol{{e}}^{\boldsymbol{{x}}} }\:+\:\boldsymbol{{C}}\:? \\ $$
Commented by CanovasCamiseros last updated on 21/Nov/20

$$\boldsymbol{{Oooooh}}!\:\boldsymbol{{I}}\:\boldsymbol{{get}}\:\boldsymbol{{it}}\:\boldsymbol{{sir}}…\:\boldsymbol{{Thank}}\:\boldsymbol{{you}}\:\boldsymbol{{so}}\:\boldsymbol{{much}}! \\ $$
Commented by CanovasCamiseros last updated on 21/Nov/20

$$\boldsymbol{{Oooooh}}!\:\boldsymbol{{I}}\:\boldsymbol{{get}}\:\boldsymbol{{it}}\:\boldsymbol{{sir}}…\:\boldsymbol{{Thank}}\:\boldsymbol{{you}}\:\boldsymbol{{so}}\:\boldsymbol{{much}}! \\ $$
