Question Number 122885 by CanovasCamiseros last updated on 20/Nov/20

Commented by CanovasCamiseros last updated on 20/Nov/20

$$\boldsymbol{{Please}}\:\boldsymbol{{help}} \\ $$
Answered by ebi last updated on 20/Nov/20
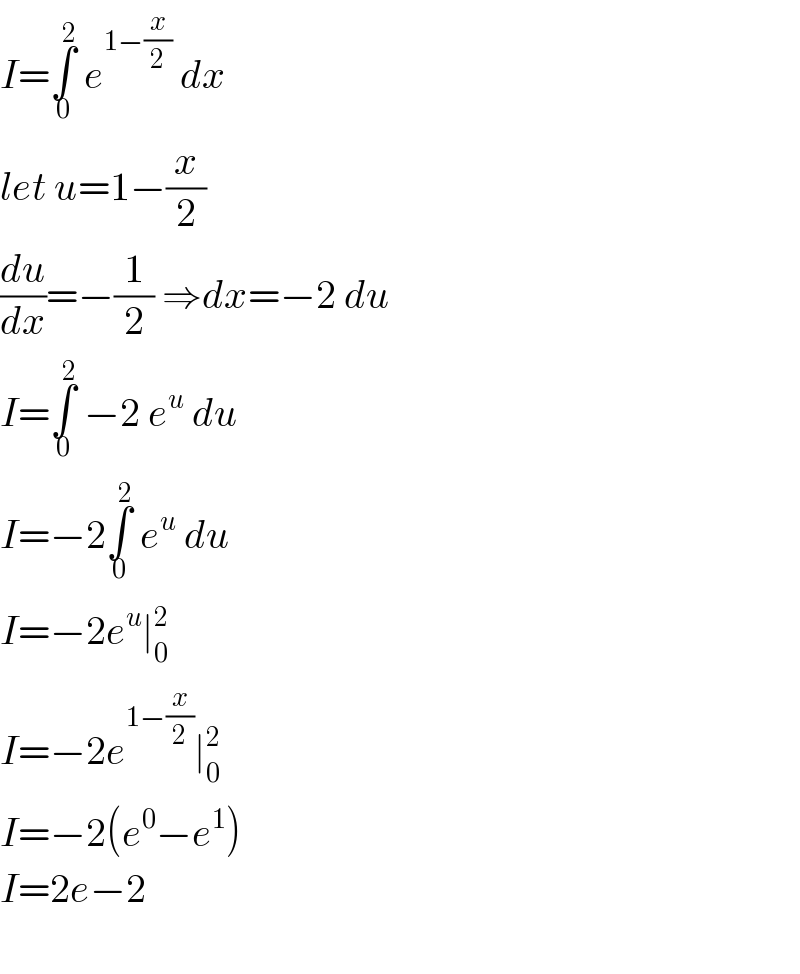
$${I}=\underset{\mathrm{0}} {\overset{\mathrm{2}} {\int}}\:{e}^{\mathrm{1}−\frac{{x}}{\mathrm{2}}} \:{dx} \\ $$$${let}\:{u}=\mathrm{1}−\frac{{x}}{\mathrm{2}} \\ $$$$\frac{{du}}{{dx}}=−\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow{dx}=−\mathrm{2}\:{du} \\ $$$${I}=\underset{\mathrm{0}} {\overset{\mathrm{2}} {\int}}\:−\mathrm{2}\:{e}^{{u}} \:{du} \\ $$$${I}=−\mathrm{2}\underset{\mathrm{0}} {\overset{\mathrm{2}} {\int}}\:{e}^{{u}} \:{du} \\ $$$${I}=−\mathrm{2}{e}^{{u}} \mid_{\mathrm{0}} ^{\mathrm{2}} \: \\ $$$${I}=−\mathrm{2}{e}^{\mathrm{1}−\frac{{x}}{\mathrm{2}}} \mid_{\mathrm{0}} ^{\mathrm{2}} \: \\ $$$${I}=−\mathrm{2}\left({e}^{\mathrm{0}} −{e}^{\mathrm{1}} \right) \\ $$$${I}=\mathrm{2}{e}−\mathrm{2} \\ $$$$ \\ $$
Answered by MJS_new last updated on 20/Nov/20

$$\int\mathrm{e}^{\mathrm{1}−\frac{{x}}{\mathrm{2}}} {dx}=\mathrm{e}\int\mathrm{e}^{−\frac{{x}}{\mathrm{2}}} {dx}=\mathrm{e}×\left(−\mathrm{2}\right)\mathrm{e}^{−\frac{{x}}{\mathrm{2}}} =−\mathrm{2e}^{\mathrm{1}−\frac{{x}}{\mathrm{2}}} +{C} \\ $$$$\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:\mathrm{2e}−\mathrm{2} \\ $$
Answered by Bird last updated on 20/Nov/20
![I=∫_0 ^2 e^(1−(x/2)) dx ⇒I=_((x/2)=t) ∫_0 ^1 e^(1−t) 2dt =2e ∫_0 ^(1 ) e^(−t) dt =2e[−e^(−t) ]_0 ^1 =2e{1−e^(−1) } =2e−2](https://www.tinkutara.com/question/Q122909.png)
$${I}=\int_{\mathrm{0}} ^{\mathrm{2}} \:{e}^{\mathrm{1}−\frac{{x}}{\mathrm{2}}} {dx}\:\Rightarrow{I}=_{\frac{{x}}{\mathrm{2}}={t}} \int_{\mathrm{0}} ^{\mathrm{1}} \:{e}^{\mathrm{1}−{t}} \:\mathrm{2}{dt} \\ $$$$=\mathrm{2}{e}\:\int_{\mathrm{0}} ^{\mathrm{1}\:} {e}^{−{t}} \:{dt}\:=\mathrm{2}{e}\left[−{e}^{−{t}} \right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\mathrm{2}{e}\left\{\mathrm{1}−{e}^{−\mathrm{1}} \right\}\:=\mathrm{2}{e}−\mathrm{2} \\ $$
